При розв'язуванні різноманітних задач фізики, хімії, математики, та інших точних наук часто користуються математичними моделями у вигляді рівнянь, що зв'язують одну або декілька незалежних змінних, невідому функцію цих змінних і похідні (або диференціали) цієї функції. Такого сорту рівняння називають диференціальними.
Якщо незалежна змінна одна, то рівняння називається звичайним; якщо незалежних змінних дві або більше, то рівняння називається диференціальним рівнянням з частинними похідними. З метою отримати високоваліфікованих спеціалістів у всіх ВУЗах де вивчають точні дисципліни обов'язковим є курс диференціальних рівнянь.
Для одних студентів теорія дається тяжко, практика ще з горем пополам, для інших важка і теорія, і практика. Якщо аналізувати диференціаьні рівняння з практичної сторони, то для їх обчислень Вам потрібно лише добре вміти інтегрувати та брати похідні. Все решта зводиться до кількох схем, які можливо зрозуміти та вивчити. Нижче Ви ознайомитеся з основними означеннями та першими простими диф. рівняннями.
Теорія диференціальних рівнянь
Означення: Звичайним диференціальним рівнянням називають рівняння, яке в собі зв'язує незалежну змінну х, функцію у(х) та похідні у'(х), уn(х) і має загальний вигляд F(x,y(x),y' (x), …, yn(x))=0
Диференцiальним рiвнянням (ДР) називається або звичайне диференцiальне рiвняння, або диференцiальне рiвняння з частинними похiдними.
Порядок диференціального рівняння визначається порядком старшої похідної (n), яка входить до даного диференціального рівняння.
Загальним розв'язком диференціального рівняння називається функція, яка містить стільки сталих, який порядок диференціального рівняння, і підстановка якої в дане диференціальне рівняння перетворює його в тотожність, тобто має вигляд y=f(x, C1, C2, …, Cn).
Загальний розв'язок, який не розв'язаний відносно у(х) і має вигляд F(x,y,C1,C2, …, Cn)=0 називається загальним інтегралом диференціального рівняння.
Розв'язок, знайдений із загального розвязку при фіксованих значеннях сталих C1,C2, …, Cn називається частинним розв'язком диференціального рівняння.
Одночасне задання диференціального рівняння і відповідної кількості початкових умов називається задачею Коші.
F(x,y,C1,C2, …, Cn)=0
y(x0)=y0;
….
yn(x0)=yn(0)
Звичайним диференцiальним рiвнянням першого порядку називається рiвняння вигляду
F(x, y, y')=0. (1)
Iнтегралом рiвняння (1) називається cпiввiдношення вигляду Φ(x, y)=0, якщо кожна неявно задана ним неперервно-диференцiйовна функцiя є розв'язком рiвняння (1).
Рівняння, яке має вигляд (1) і не може бути зведене до простішого вигяду називається рiвнянням, нерозв'язним стосовно похiдної. Якщо його можна записати у виглядi
y' = f(x,y), то воно називається рiвнянням, розв'язаним стосовно похiдної.
Задача Коші для рівняння першого порядку містить лише одну початкову умову і має вигляд:
F(x,y,y')=0
y(x0)=y0.
Рiвняння вигляду
M(x,y)dx+N(x,y)dx=0 (2)
де змiннi x i y є "симетричними": можна припускати, що x – незалежна, а y – залежна змiнна, або, навпаки, y – незалежна, а x – залежна змiнна, називається рiвнянням в симетричнiй формі.
Геометричний зміст диференціаьного рівняння першого порядку
y'=f(x, y) (3)
полягає в наступному.
Дане рівняння встановлює зв ' язок ( залежність ) між координатами точки (x; y) і кутовим коефіцієнтом y' дотичної до інтегральної кривої, що проходить через цю точку . Таким чином, рівняння y'=f(x, y) дає сукупність напрямів ( поле напрямів ) на декартовій площині Oxy.
Крива, побудована на точках, в яких напрям поля однаковий, називається ізокліною. Ізоклінами можна користуватися для наближеної побудови інтегральних кривих . Рівняння ізокліни можна одержати, якщо покласти похідну рівну сталій y'=С
f(x, y)=С - рівняння ізокліни.
Iнтегральною лiнiєю рiвняння (3) називається графiк розв'язку цього рiвняння.
Звичайнi диференцiальнi рiвняння, розв'язки яких можна задати аналітично y=g(x), називаються iнтегровними рiвняннями.
Рiвняння вигляду
M0(x)dx+N0(y)dy=0 (3)
називаються рiвняннями з вiдокремленними змiнними.
З них і розпочнемо знайомство з диференціальними рівняннями. Процес знаходження розв'язків диференціального рівняння ще називають інтегруванням диференціального рівняння.
Рівняння з відокремленими змінними
Приклад 1. Знайти розв'язок рівняння y'=x .
Виконати перевірку розв'язку.
Розв'язання: Запишемо рівняння в диференціалах
dy/dx=x або dy=x*dx.
Проінтегруємо праву та ліву частини рівняння
int(dy)=int(x*dx);
y=x2/2+C.
Це і є загальний інтеграл ДР.
Перевіримо його правильність, обчислимо похідну функції
y'=1/2*2x+0=x.
Як ожна переконатися, отримали вихідне ДР, отже обчислення виконані правильно.
Ми тільки що знайшли розв'язок диференціального рівняння першого порядку. Це саме простіше рівняння, яке можна собі уявити.
Приклад 2. Знайти загальний інтеграл диференціального рівняння
(x+1)y'=y+3
Розв'язання: Запишемо вихідне рівняння в диференціалах
(x+1)dy=(y+3)dx.
Отримане рівняння зводимо до ДР з відокремленими змінними
![]()
Все що залишилося це взяти інтеграл від обох частин
![]()
За табличними формулами отримаємо
ln|y+3|=ln|x+1|+C.
Якщо експонувати обидві частини, то отримаємо
y+3=e ln|x+1|+C або y=e ln|x+1|+C-3.
Такий запис є правильним, але не є компактним.
На практиці застосовують інший прийом, при обчисленні інтегралу сталу вносять під логарифм
ln|y+3|=ln|x+1|+ln(C).
За властивостями логарифма це дозволяє згорнути два останні доданки
ln|y+3|=ln(С|x+1|).
Тепер при експонуванні розв'язок диференціального рівняння матиме набагато красивіший і читабельний вигляд
y= С|x+1|+3
Запам'ятайте дане правило, на практиці воно застосовується як еталон обчислень.
Приклад 3. Розв'язати диференціальне рівняння
y'=-y*sin(x).
Розв'язання:Запишемо рівняння в диференціалах
dy/dx= y*sin(x)
або після перегрупування множників у вигляді рівняння з відокремленими змінними
dy/ y=-sin(x)dx.
Залишилося проінтегрувати праву та ліву частини рівняння
int(1/y,y)=-int(sin(x), x);
ln|y|=cos(x)-ln(C).
Константу зручно внести під логарифм, та ще й з від'ємним значенням, щоб перенісши в ліву частину отримати
ln|С*y|=cos(x).
Експонуємо обидві частини залежності
С*y=exp(cos(x)).
Це і є загальний інтеграл диференціального рівняння.
Його можна залишити як є, а можна сталу перенести в праву сторону
![]()
Обчислення не складні, інтеграли теж в бльшості випадків можна знайти за табличними формулами інтегрування.
Приклад 4. Розв'язати задачу Коші
y'=y+x, y(1)=e3-2.
Розв'язання:Тут вже попередні перетворення не пройдуть. Проте рівняння лінійне і досить просте. В таких випадках потрібно ввести нову змінну
z=y+x.
Пам'ятаючи, що y=y(x) знайдемо похідну від z.
z'= y'+1,
звідки виражаємо стару похідну
y'= z'-1.
Підставимо це все у вихідне рівняння
z'-1=z або z'=z+1.
Розпишемо диф. рівняння через диференціали
dz=(z+1)dx.
Відокремлюємо змінні в рівнянні
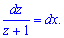
Залишилося обчислити прості табличні інтеграли, які під силу кожному
![]()
Експонуємо залежність, щоб позбутися логарифма при функції
z+1=ex+Сабо z=ex+1-1
Не забуваємо повернутися до виконаної заміни
z=x+y= ex+С-1,
звідси виписуємо загальний розв'язок диференціального рівняння
y= ex+С-x-1.
Знайти розв'язок задачі Коші до ДР в даному випадку не складно. Виписуємо умову Коші
y(1)=e3-2
та підставляємо у тільки що знайдений розв'язок
e1+С-1-1= e3-2.
Звідси отримаємо умову для обчислення сталої
1+С=3; С=3-1=2.
Тепер можемо записати розв'язок задачі Коші (частковий розв'язок ДР)
y= ex+2-x-1.
Якщо Ви добре вмієте інтегрувати, з похідної у Вас справи теж на висоті, тоді тема диференціальних рівнянь для Вас не буде перешкодою в навчанні..
В подальшому навчанні Вам необхідно вивчити декілька важливих схем, щоб навчитися розрізняти рівняння та знати, яка заміна чи методика працює в кожному випадку.
Після цього на Вас чекають однорідні та неоднорідні диференціальні рівняння першого та вищих порядків. Щоб не навантажувати Вас теорією в наступних уроках ми будемо наводити лише тип рівнянь та коротку схему їх обчислень. Всю теорію Ви можете почитати з методичок для вивчення курсу "Диференціальні рівняння" або онлайн ресурси, що містять зрозумілі Вам пояснення теорії диференціальних рівнянь.
Готові відповіді з диф. рівнянь взяті з програми дя математиків ЛНУ ім. І. Франка.
Ми знаємо, як розв'язати диференціальні рівняння і постараємося в легкий спосіб прищепити ці знання Вам!


