В попередній статті розглянуті більш прості приклади на типи поверхні другого порядку. В цій та наступних публікаціях наведено аналіз багатьох прикладів, що повністю пояснює можливі алгоритми їх обчислень.
Задача 6.2.2 Визначте тип поверхні другого порядку:
б) x2-3y2+4zx-2yz=0;
Розв'язання: Виконуємо маніпуляції з квадратичними записами, щоб в підсумку отримати повні квадрати 
Щоб спростити рівняння поверхні виконуємо заміну змінних:

тоді отримаємо більш компатний запис

Рівняння описує конус.
Задача в) Визначте тип поверхні другого порядку:
x2+4y2+z2-4xy-4yz+2xz=0;
Розв'язання: Тут, щоб виділити повні квадрати доведеться вдатия до математичних хитрощів, а все тому, що перед xy маємо знак мінус. Запишемо перетворення
x2+(-2y)2+z2+2x(-2y)+2xz+2(-2y)z=0;
(x-2y+z)2=0.
Без знання формул скороченого множення цей приклад досить довго довелось би розписувати, тому вчіть їх. Чим краще Ви будете ними володіти, тим легше Ви знайдете їм застосування.
Таким чином, отримали дві дійсні площини x-2y+z=0, що збігаються.
Задача г) Звести до канонічного вигляду рівняння поверхні другого порядку:
x2+5y2+z2+2xy+6xz+2yz-2x+6y-10z=0;
Розв'язання: В цьому завданні не все так легко, як Вам би того хотілося. Метод Лагранжа дасть хороший результат, але до нього ще потрібно дійти.
Тому першим ділом розписуємо рівняння, щоб виділити повні квадрати. Цього разу за добутком змінних потрібно виділити квадрат суми 4 доданків
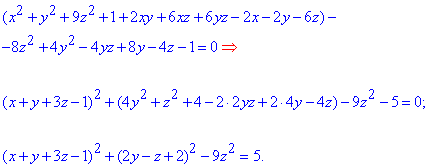
Залишилося зробимо заміну:
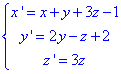
і ми отримаємо
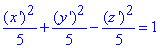
канонічне рівняння однополого гіперболоїда.
Можливо Вам здається , що приклад занадто важкий, проте хто вчиться на факуьтетах з математичним нахилом (математики, прикладники, фізики) на практиці можуть зустріти ще важчі завдання. І повірте, що викладачі, аж ніяк не заінтересовані, щоб Ви швидко навчилися їх рішати.
Задача д) Звести до канонічного вигляду рівняння поверхні другого порядку:
4x2+2y2+10z2-4xy+12xz-8yz=0;
Розв'язання: Як і у попередньому завданні, виділяємо суму квадратів трьох змінних, враховуючи множники при xy, xz, zy. І хоч це завдання не з легких, Ви маєте навчитися їх обчислювати.
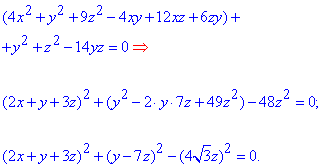
Далі зробимо заміну змінних:
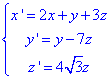
і отримаємо
(x')2+(y')2-(z')2=0.
канонічне рівняння конуса.
Це і є тип поверхні, який потрібно було визначити.
Змінимо дещо умову, а саме знак перед останнім доданком.
Задача д) Звести до канонічного вигляду поверхню:
4x2+2y2+10z2-4xy+12xz+8yz=0;
Розв'язання: Це призведе до того, що поміняється невелика частина рівняння поверхні, однак при зведенні до повних квадратів отримаємо не три, а два доданки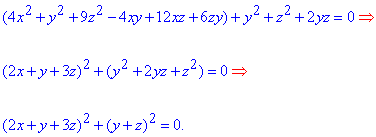
Заміна змінних:
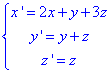
перетворить рівняння поверхні до вигляду
(x')2+(y')2=0.
Повірте, що це не рівняння кола, як багато кому з Вас здається.
Отримали канонічне рівняння двох уявних площин, що перетинаються по дійсній прямій.
Задача е) Визначте тип поверхні другого порядку:
4x2+9y2+z2-12xy+4xz-6yz+4x-6y+2z-5=0;
Розв'язання: Порозписуємо коефіцієнти при змінних в квадраті, щоб бачити в якоу напрямі перетворювати рівняння заданої поверхні
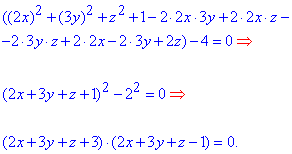
Маніпуляції не всім очевидні, проте правильні. Передостанню формулу розписуємо за різницею квадратів
В підсумку отримали дві дійсні паралельні площини
2x+3y+z+3=0;
2x+3y+z-1=0.
За зворотнім ходом поступають викладачі, придумуючи студентам нові завдання. Беруть два рівняння площин з простими коефіцієнтами при змінних, перемножують їх, і мають нове завдання на поверхні, щоб перевірити як добре Ви знаєте теоретичний матеріал.
Задача є) Звести до канонічного вигляду рівняння поверхні другого порядку:
x2-2y2+z2+4xy-8xz-4yz-14x-4y+14z+16=0;
Розв'язання: Перегрупуємо доданки, щоб використати формули скороченого множення.
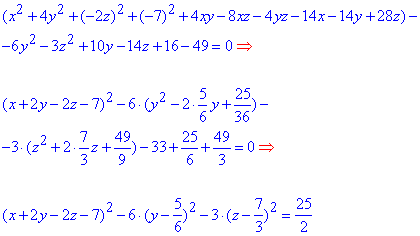
Перехід від першого до другого запису найбільш важчий, тож спробуйте в ньому розібратися самостійно.
Подаьше виділення повних квадратів під силу більшості студентів.
Щоб спростити запис зробимо заміну:
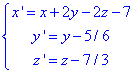
тоді рівняння поверхні 2 порядку спроститься до виду
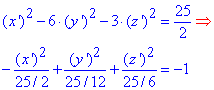
Отримали рівняння двополого гіперболоїда.
Задача ж) Визначте тип поверхні другого порядку:
2x2+y2+2z2-2xy-2yz+x-4y-3z+2=0;
Розв'язання: Методика визначення типу поверхні з прикладу в приклад тільки ускладнюється і дане завдання не вийняток.
Щоб не повторюватися наведемо всі формули перетворень, а Ви вже аналізуйте, що і для чого потрібно згруповувати
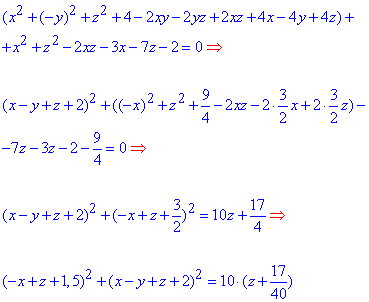
В результаті рівняння поверхні другого порядку стане більш читабельним.
Останній штрих вносить наступна заміна змінних
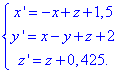
яка дозволяє в формулі
(x')2+(y')2=10z'.
побачити рівняння еліптичного параболоїда.
Задача з) З'ясуйте тип поверхні другого порядку:
x2+5y2+z2+2xy+6xz+2yz-2x+6y+2z=0.
Розв'язання: Виконуємо маніпуляції, щоб розділити змінні та звести рівняння поверхні другого порядку до канонічного вигляду
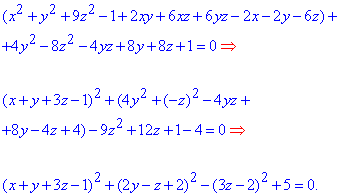
Після виділення повних квадратів залишилося зробимо заміну змінних:
x'=x+y+3z-1;
y'=2y-z+2;
z'=3z-2
і поверхня набуде вигляду
(x')2+(y')2-(z')2=-5.
Рівняння описує двополий гіперболоїд.
На цьому завдання на зведення до канонічного вигляду рівняння поверхні не закінчуються, більше тако сорту прикладів шукайте на сторінках сайту.


