Продовжуємо вивчати правила розкриття невизначеностей в границях. Сьогодні розглянемо 5 прикладів та проаналізуємо хід обчислень.
Приклад 6. Обчислити границю послідовності:
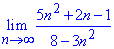
Розв'язання: При підстановці безмежності дістанемо невизначеність типу безмежність поділити на безмежність.
Розкрити особивість можна двома способами: за правилом Лопіталя або виділенням множників, що вносять найбільший вклад в чисельнику та знаменнику.
За правилом Лопіталя отримаємо
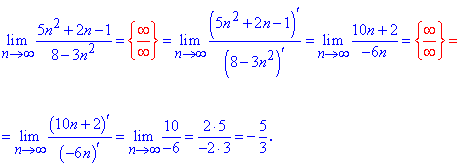
За другою методикою границя послідовності рівна
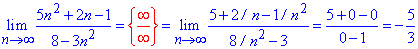
Значення співпадають, як перша схема так і друга не важкі.
Проте часто в одних завданнях вимагають обчислити границю послідовності за правилом Лопіталя.
В інших навпаки – не використовуюси формули Лопіталя.
Приклад 7. Обчислити границю послідовності:
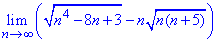
Розв'язання: Маємо різницю двох коренів, які при підстановці змінної дають особливість типу безмежність мінус безмежність.
Для усунення особливості домножимо та поділимо кореневу залежність на спряжений вираз (суму коренів). В результаті прийдемо до різниці квадратів в чисельнику.
Повторна підстановка дає особливість виду безмежність розділити на безмежність.
Щоб позбутися особливості виділяємо домінантні множники в чисельнику та знаменнику та оцінюємо, що в підсумку переважує (домінує).
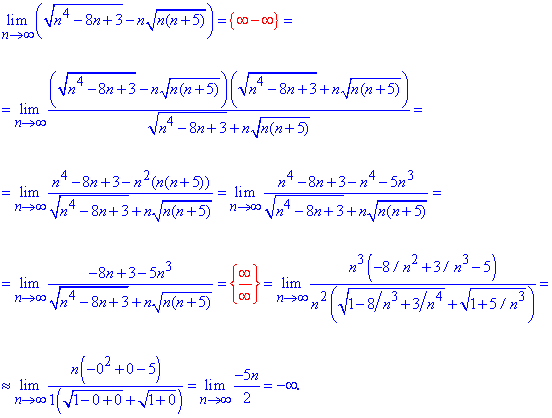
Отримали, що в чисельнику старший степінь ніж в знаменнику, тому границя прямує до безмежності. Але важливо ще з'ясувати чи до плюс нескінченності чи до мінус нескінченності. Для цього слід проаналізувати вклад доданків у дужках.
Приклад 8. Знайти границю функції:
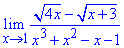
Розв'язання: При підстановці одиниці отримуємо особливість типу нуль розділити на нуль {0/0}.
Для її розкриття різницю коренів в чисельнику домножимо на суму коренів, щоб позбутися ірраціональності. На ту ж суму коренів слід домножити знаменник, щоб маніпуляціями не змінити значення границі.
Далі аналізуємо знаменник – він містить поліном, який в свою чергу має в розкладі множник (x-1) (як особливість).
Розкладемо поліном на прості множники та замінимо ними відповідну частину дробу.
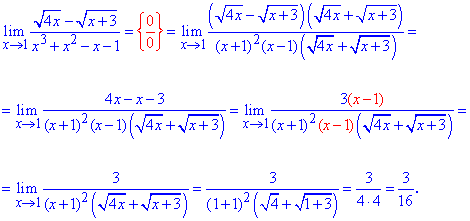
Далі чисельник та знаменник спрощуємо на спільний множник (x-1), та методом підстановки знаходимо границю функції, що залишилася.
Приклад 9. Знайти границю функції:
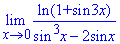
Розв'язання: У завданнях де змінна прямує до нуля і маємо дріб, що містить логарифми чи тригонометричні функції варто шукати можливість отримати першу чудову границю, наслідки другої та першої границь або поєднання обох варіантів. Цей приклад поєднує все можливе, що може Вас чекати на практиці.
Проста підстановка показує, що маємо границю типу {0/0}. Для усунення невизначеності та зведення спершу логарифма до вугляду ln(1+y)/y розділимо та помножемо на sin(3x). Щоб цей же синус в чисельнику звести під якусь формулу, розділимо та помножимо на (3x). Таким чином отримаємо частину, яка відповідає за формулу першої чудової границі.
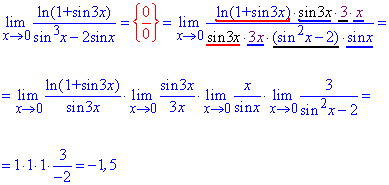
Різницю синусів, що була на початку в знаменнику дробу розпишемо, виділивши sin(x) як спільний множник.
Далі переходимо до добутку границь, погрупувавши попередньо відповідні дроби під формули чудових границь.
Всі решта відповіді, які Вас цікавлять дає наведена формула розрахунків.
Приклад 10. Знайти границю функції:
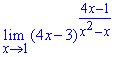
Розв'язання: Пряма підстановка одиниці показує, що маємо границю типу одиниця в степені безмежність. А це означає, що маємо справу з другою чудовою границею.
Для усунення особливості в дужках та показнику виділимо вирази, що містять (x-1). Після цього робимо заміну змінних, t=x-1, при цьому нова змінна прямуватиме до нуля. Далі в показнику виділяємо множник, який є обернено пропорційним до доданку в дужах (1/4t), це дасть нам експоненту.
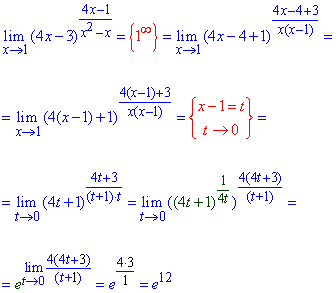
Все, що залишиться множником в показнику дасть степінь експоненти в граничному переході (12).
Добре проаналізуйте наведений приклад, він насправді не такий важкий, якщо уважно розібратися.
В нових публікаціях Ви отримаєте відповіді на інші питання, які могли у Вас виникнути у зв'язку з тим, що розглянуто всього 5 прикладів.


