Приклади границь, що містять невизначеності виду нуль розділити на нуль (0/0) часто зустрічаються у тригонометричних функціях. Для їх розкриття використовують першу чудову (особливу) границю, суть якої полягає в тому, що границя відношення синус функції до аргументу, коли той прямує до нуля рівна одиниці
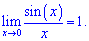
На її основі можна отримати ряд корисних для практики наслідків першої границі
1) 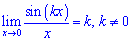
2) 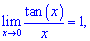
3) 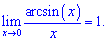
Друга особлива границя дозволяє розкривати невизначеності виду одиниця в степені безмежність 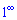 .
.
Формула другої чудової границі наведена нижче
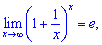
де e=2,71828182849045... – експонента.
На основі другої особливої границі отримують наступні формули (наслідки 2 границі)
1) 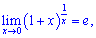
2) 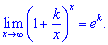
Завдання на границі, які зводяться до першої та другої особливих (чудових) границь зустрічаються доволі рідко, однак без наведених формул такі приклади не розв'язати. Розглянемо деякі приклади із збірника задач Дубовика В.П., Юрика І.І. "Вища математика", що приводять до застосування особливих границь.
Приклад 1. Знайти границю фунціїй.
1) (4. 388) 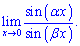
Розв'язок. Помножимо чисельник і знаменник на аргумент та зведемо до першої чудової границі
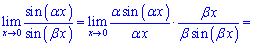
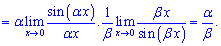
Для одних це легко побачити, іншим важко зрозуіти схему обчислень. А її суть в отриманні запису sin(x)/x, все що буде при цьому множником і буде складати границю функції.
2) (4. 393) 
Розв'язок. Поділимо чисельник і знаменник на змінну x. В результаті і там і там отримаємо "число" + наслідок перої особливої границі
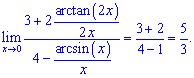
Настільки легко можна обчислювати, якщо мати шпаргалку та знати, що потрібно шукати.
3) (4. 399) 
Розв'язок.Згідно формули розвинення кореня в околі одиниці в ряд
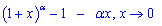
знаменник дробу можна перетворити наступним чином
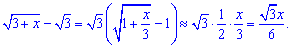
На основі цього знаходимо границю функції
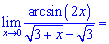
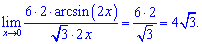
В чисельнику фігурував арксинус подвійного аргументу, тому для зведення під правило першої границі подвійний аргумент виділяємо також в знаменнику. Далі виписуємо границю у вигляді ірраціонального числа та, домноженням чисельника і знаменника на корінь з 3, приводимо запис до коректного вигляду.
4) (4. 432) 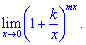
Розв'язок.Зведемо показникову функцію під правило другої визначної границі. Для цього в степені утворємо множник обернено пропорційний до доданку в дужках.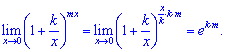
Все що залишиться і буде степенем експоненти. Застосовуйте цю властивість показників у подібних завданнях на границі.
5) (4. 437) 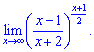
Розв'язок. В такого роду завданнях функцію слід звести під формулу другої визначної границі.
Для цього зведемо до правильного дробу вираз в дужках
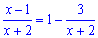
та підставимо в границю. Після розділення показників отримаємо добуток двох границь
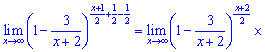
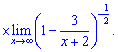
Спростимо перший множник
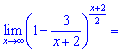
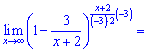
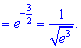
Друга границя рівна одиниці
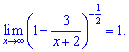
Просьба не вважати її чимось схожим на другу границю, в показнику немає аргументу "х", а вираз в дужках прямує до одиниці.
В результаті множення отримаємо
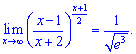
6) 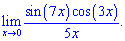
Розв'язок. Зведемо до першої визначної границі.
Тут зразу можна здогадатися, що косинус ніякого вкладу не внесе, оскільки в нулі рівний одиниці. Залишається в знаменнику отримати 7x
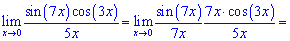
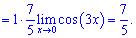
Після незначних перетворень границя функції рівна 7/5.
7) 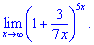
Розв'язок. Перетворимо показник для того, щоб можна було застосувати другу визначну границю.
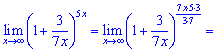
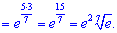
Перетворення дробу в показнику не складне і в результаті обчислень отримаємо e15/7.
Подібних прикладів можна навести сотні. Їх розв'язування дозволить закріпити Вам кращі практичні навички, тож пробуйте розв'язувати самостійно. Якщо в навчанні Вам зустрінуться важкі границі, порахувати які Ви не в змозі, звертайтеся до нас. Ми Вам в цьому допоможемо!
Переглянути подібні матеріали


