Рангом матриці називається найвищий порядок відмінних від нуля мінорів. Його позначають через r або rang(A).
ВЛАСТИВОСТІ РАНГУ МАТРИЦІ
1. Ранг матриці рівний нулю лише для нульової матриці. В інших випадках ранг матриці рівний деякому додатному числу.
2. Ранг прямокутної матриці не перевищує меншого із двох чисел m і n, тобто ![]()
3. Для квадратної матриці n-го порядку r=n тільки тоді, коли матриця невироджена.
4. У випадку квадратної матриці, якщо r<n то визначник матриці дорівнює нулю.
При знаходженні рангу матриці, як правило, треба обчислювати велику кількість визначників. Щоб полегшити задачу студентам давно-давним знайдені елементарні перетворення за допомогою яких можна, злегка помінявши вигляд матриці, без обчислення визначників порахувати ранг.
ЕЛЕМЕНТАРНІ ПЕРЕТВОРЕННЯ
1. Транспонування, тобто заміна кожного рядка стовпчиком з тим ж номером і навпаки.
2. Перестановка двох рядків або двох стовпчиків.
3. Множення всіх елементів рядка або стовпчика на будь-яке число не рівне нулю.
4. Додавання до всіх елементів рядка або стовпчика відповідних елементів паралельного ряду, помноженого на одне і те ж число.
Матриці, одержані одна з другої елементарними перетвореннями, називаються еквівалентними. Еквівалентні матриці не рівні одна одній, але при елементарних перетвореннях матриці її ранг не змінюється. Якщо матриці A і B еквівалентні, то це записують так: ![]()
Розглянемо два основних методи знаходження рангу матриці.
Перший метод – метод окантування – полягає у наступному:
Якщо всі мінори І-го порядку, тобто елементи матриці, рівні нулю, то r=0.
Якщо хоч один із мінорів 1-го порядку не дорівнює нулю, а всі мінори 2-го порядку дорівнюють нулю, то r=1.
Якщо мінор 2-го порядку відмінний від нуля, то досліджуємо мінори 3-го порядку. Таким способом знаходять мінор k-го порядку і перевіряють, чи не дорівнюють нулю мінори k+1-го порядку.
Якщо всі мінори k+1-го порядку дорівнюють нулю, то ранг матриці A(aij)m,n дорівнює числу k. Такі мінори k+1-го порядку, як правило, знаходять шляхом "окантування " мінора k-го порядку.
Другий метод визначення рангу матриці полягає в застосуванні елементарних перетворень матриці при зведенні її до діагонального вигляду. Ранг такої матриці дорівнює кількості відмінних від нуля діагональних елементів.
Розглянемо приклади застосування кожного методу.
Приклад 1. Знайти ранг матриці A методом окантування.
![]()

Розв'язок. Матриця A(aij)4,5 містить ненульові елементи мінори 1-го порядку, отже її ранг може бути рівний одиниці. Згідно правила ранг матриці не перевищує чотирьом r<=4. Мінор 2-го порядку
![]()
рівний нулю, але наступний мінор
![]()
відмінний від нуля. Окантовуючи мінор другого порядку перевіримо третій: для цього розкладемо його по третьому стовпчику
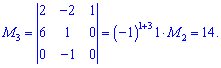
Розглянемо мінор четвертого порядку, що окантовує даний
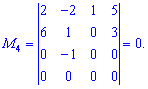
Він рівний нулю, оскільки останній рядок нульовий. Лишається обчислити ще один мінор
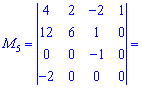
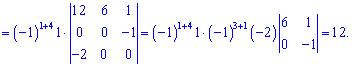
Шуканий ранг матриці рівний чотирьом (r=4). На прикладі можна бачити, що вибір окантування не завжди можна вдало вибрати і потрібно числити велику кількість мінорів.
Приклад 2. Знайти ранг матриці A.
![]()

Розв'язок. 1. Переставимо четвертий стовпець на перше місце, а всі решта змістимо вправо.
2. Занулимо всі елементи в першому рядку після 1. Для цього до 2,3,4,5 стовпців додамо перший помножений на -3; -2; 2; -5 відповідно.
3. Третій стовпець поділимо на 6. До четвертого і п'ятого стовпців додамо третій, помножений на -1;-3.
4. До п'ятого стовпця додамо четвертий, помножений на 2.
5. Переставимо третій і четвертий стовпці на друге і третє місця, а другий стовпець на місце четвертого.
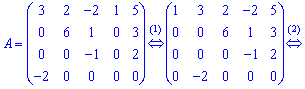
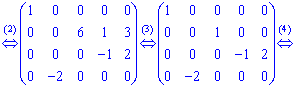
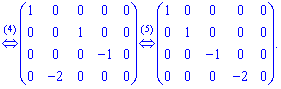
В вихідній матриці викреслемо останній стовпець з нульовими елементами
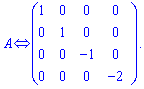
Ранг еквівалентної матриці рівний чотирьом, а отже і rang(A)=4. Можна заміти, що матриці в першому і другому прикладах еквівалентні між собою (мають однакові ранги). Таим методом обчислють ранги набагато біьших за розміром матриць, є алгоритми, які дозволяють автоматизувати перевірку рангу матриць і створити корисні для використання калькуятори.
Вас може зацікавити:


