Для обчислення системи рівнянь часто доцільно використовувати метод Крамера. Він передбачає обчислення визначників матриць, іншого застосування визначникам важко придумати.
На питання "Яка матриця має визначник?" можна відповісти коротко і однозначно – квадратна. Не можна знайти визначник прямокутної матриці, таких формул Ви просто не знайдете.
А зараз дамо визначення, що таке визначник та наведемо на прикладах основні його властивості, що на практиці дозволяють спростити їх знаходження. означення
Означення визначника: Визначником (детермінантом) будь-якої квадратної матриці A=(ai,j) називається алгебраїчна сума всіх можливих добутків елементів матриці ai,j, взятих по одному з кожного рядка і стовпця з певним знаком. Цей знак рівний мінус одиниці (-1) в степені кількості інверсій номерів других індексів, коли перші впорядковані в порядку зростання.
Таке правило незручне для сприйняття, тому на практиці користуються простими формулами.
Визначник другого порядку рівний різницю добутків елементів головної та бічної діагоналі:

Визначник третього порядку знаходять за правилом трикутників:
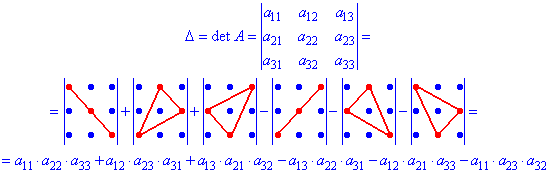
Визначник 3 порядку має 6 доданків з трьох множників у кожному. Формула для визначника четвертого порядку ще складніша і містить 4!=4*3*2=24 доданки, визначник п'ятого порядку утворюється сумуванням 5!=120 доданків, кожен з яких є добутком 5 елементів матриці, взятих відповідно до означення.
Але на практиці визначники 4, 5 порядку теж не обчислюють за загальними формулами, а розкладають через мінори або спрощують, застосовуючи елементарні перетворення над визначниками.
Останні базуються на властивостях визначників, які продемонструємо на прикладах.
Властивості визначників матриць
1. Визначник залишається незмінним при його транспонуванні (тобто заміна рядків на стовпці і навпаки не змінює результуюче значення).
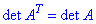
Доведення продемонструємо на прикладі визначника 2 порядку
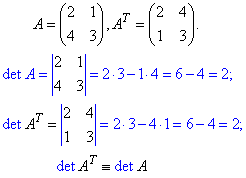
2. Якщо всі елементи деякого рядка чи стовпця визначника дорівнюють нулю, то і сам визначник дорівнює нулю.
Це доведемо без наведення прикладів – справа в тому, що кожен доданок у визначнику має елементи з кожного рядка і стовпця. Звідси слідує, що у кожній сумі буде множник рівний нулю, і відповідно сам визначник теж.
3. Якщо у визначнику замінити місцями два сусідні рядки чи стовпці, то визначник змінить знак на протилежний. Важливим тут є слово сусідні, оскільки якщо змінити 1 і 2 рядки то матимемо –det(A), якщо 1 і 3 то знак зміниться двічі, а два рази –(–) рівний (+), матимемо det(A).
4. Значення визначника залишиться тим самим, якщо до будь-якого рядка (стовпця) додати інший, помножений на довільне число або лінійну комбінацію інших рядків.
Суть цього правила в тому, що всередині визначника можна виконувати певні маніпуляції, але при цьому не можна нічого робити з рядком чи стовпцем над яким робимо ці перетворення.
Для прикладу, нехай маємо матрицю 3 порядку з наступними елементами
A(1, 2,3; 4,5,7;3,3;1).
Якщо знайти детермінант матриці A за правилом трикутника, то він рівний det(A)=9.
Але при цьому буде чимало обчислень, тому спробуємо занулити частину елементів.
Для цього від друго рядка віднімемо перший, і в отриманій матриці від третього рядка віднімемо другий.
В результаті елементарних дій матриця перетвориться до наступної
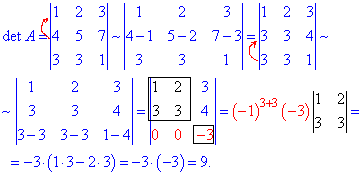
Тут наприкінці було використано розклад визначника через алгебраїчні доповнення до 3 рядка.
Оскільки два елементи =0, то лише третій вносить вклад.
Отже маємо det(A)=9, що рівно значенню за правилом трикутників.
А тепер порівняйте скільки операцій множення та сумування потрачено при кожному з варіантів і Ви зрозумієте, що часто другий метод є швидший і в нього менша статистика допущення помилок при розрахунках. При знаходженні визначниів четвертого та вищіх порядків даний метод показує кращу ефективність ніж, для матриць 2, 3 порядку.
З цієї властивості випливають наступні.
5. Визначник у якого рівні два однакові рядки чи стовпці дорівнює нулеві.
Як доведення можна сказати, що над одним з рядків (стовпців) визначника можна виконати перетворення описані в попередньому пункті. Таким чином один рядок (стовпець) матиме нульові елементи, що за 2 властивістю веде до det(A)=0.
Наприклад
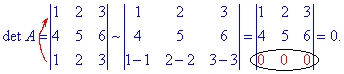
6. Спільний множник можна винести з рядка чи стовпця визначника і записати його перед визначником.
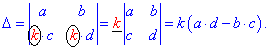
Правило використовують, коли при елементарних перетвореннях слід змінювати рядок (стовпець), який модифікуємо. Тоді при домноженні на можник (k), він автоматично йде в заменник дробу перед визначником. Інше застосування полягає в зменшенні трудоємкості обчислень при великих значеннях елементів матриці. Для прикладу
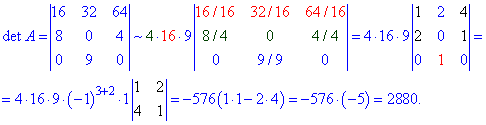
Тут правило винесення спіьного множника до рядка використано тричі + застосовано розклад визначника через алгебраїчні доповнення до третього рядка, що вилилося в обчислення одного мінору 2 порядку.
Таким чином знайшли визначник і він рівний det(A)=2880.
А тепер прикиньте, скільки потрібно обчислень, якщо не використовувати калькулятор, щоб отримати таке значення.
Інше трактування правила - якщо деякий рядок чи стовпець детермінанта помножити на довільне число (k) , то значення визначника зміниться у (k) разів.
7. Сума попарних добутків елементів деякого рядка чи стовпця на відповідні алгебраїчні доповнення до іншого рядка чи стовпця визначника рівна нулеві.

Властивість доводити не будемо, оскільки на практиці Ви цю властивість навряд чи застосуєте.
8. Якщо елементи будь-якого рядка (стовпця) визначника записати у вигляді суми, то цей визначник можна подати у вигляді суми відповідних визначників.
Наприкад
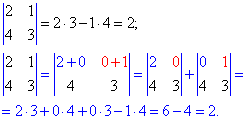
З цієї формули вивести наступну формулу.
9. Розклад визначника через елементи рядка чи стовпця
Визначник рівний сумі добутків елементів будь-якого рядка (стовпця) на алгебраїчні доповнення до таких елементів.
Для матриці 3 порядку розклад визначника за 2 рядком матиме вигляд
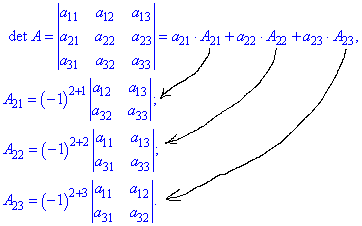
Ця властивість є архіважливою при розписанні визначників 4, 5 порядку через алгебраїчні доповнення, що дозволяє понизити на одиницю порядок шуканих визначників. Так, замість одного визначника 4 порядку, потрібно знайти 4 визначники четвертого порядку.
Таких прикладів мало, однак без знання формул розкладу важко знайти кінцеве значення.
Також, як частковий випадок наведемо ще дві корисних властивості.
10. Для верхньої трикутної чи нижньої трикутної матриці визначник рівний добутку діагональних елементів.
Доведення не потребує, оскільки просто перевірити із загальних формул.
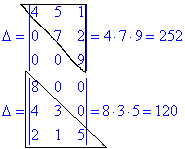
11. Подібне до попереднього, тільки стосується бокової діагоналі. Якщо у визначнику елементи над (під) боковою діагоналлю рівні нулю то він рівний добутку елементів діагоналі, взятим зі знаком «мінус».
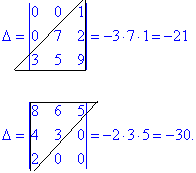
Останні два правила корисні, оскільки на практиці часто зустрічаються розріджені чи блочні матриці, які через елементарні перетворення рядків чи стовпців не важко звести до трикутного вигляду. Всі подальші обчисення зводяться до множення діагональних елементів.
Вчіть правила та вдало застосовуйте на практиці!
Вас може зацікавити:


