Задачі на складні відсотки розв'язуються в досить швидкий спосіб при знанні декількох простих формул. Частина з них стосується нарахувань по внеску чи кредиту, коли ті здійснюються за певні часові проміжки. Також складні відсотки використовують в задачах хімії, медицини та ряді інших.
ФОРМУЛИ СКЛАДНИХ ВІДСОТКІВ
У випадку розміщення вкладів з капіталізацією відсотків на роки кінцева сума депозиту визначається формулою
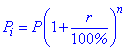
Тут P – початковий внесок, r – відсоткова ставка, n – кількість років. За складними відсотками працюють банки, івестиційні фонди, страхові фірми. Поширені за кордоном, а зараз і в Україні - пенсійні фонди та фонди страхування життя працюють за схемою складних відсотків.
При розміщенні вкладів з капіталізацією відсотків поквартально формула складних відсотків матиме вигляд
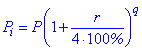
де q – кількість повних кварталів.
При капіталізації відсотків щомісячно застосовують наступну формулу для обчислень
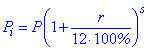
де s – кількість місяців існування угоди.
Останній випадок, неперервне нарахування відсотків, коли складні відсотки нараховують щоденно, розраховують за формулою
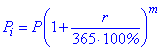
де m – кількість днів.
Страхування життя та відкладання пенсій відбувається за складнішими формулами, крім нарахування складних відсотків щороку здійснюються необхідні внески.
Розглянемо два випадки накопичення. Чоловік відкладає 5000 грн. протягом 20 років. За цей час він відкладе
20*5000=100000 (грн).
При відкладанні у накопичувальні фонди з річною ставкою 13%, за перший рік сума зросте до
5000*(1+13/100)=5650 (грн)
Наступного року чоловік до даної суми додає ще 5000 грн. В результаті, за другий рік сума збільшиться
(5650+5000)*(1+0,13)=12034.50 (грн)
Продовжуючи подібні обчислення, вкінці терміну отримаємо суму розміром 457349,58 грн.
Повірте – помилок при обчисленні немає, велике значення набігає за рахунок складних відсотків. Сумнівним лишається тільки історія зміни платоспроможності гривні через 20 років. Враховуючи політику держави вкладати гроші в такі фонди люди не спішать, проте за кордоном практика відкладання грошей поширена, правда відсоткові ставки набагато нижчі.
Розглянемо поширені задачі на складні відсотки.
Задача 1. Вкладник поклав на депозит $3000 під 9% річних на 10 років. Яка сума акумулюється наприкінці 10-го року при річній капіталізації? На скільки зросте сума порівняно з початковим внеском?
Розв'язання:
Застосовуємо формулу складних відсотків для знаходження суми наприкінці терміну
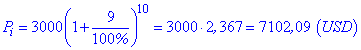
Щоб дати відповідь на друге питання, від значення 7102,09 віднімаємо суму вкладу.
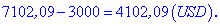
Різниця становить 4102 долари.
Задача 2. Інвестор вклав 7000 грн під 10% річних при умові нарахування складних процентів щокварталу. Яку суму він отримає через 8 років?
Розв'язання:
Застосовуємо 2 формулу складних відсотків. Знаходимо кількість кварталів
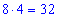
та підставляємо у формулу
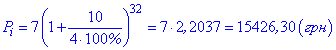
Шкільні задачі на складні відсотки
Для прикладу, візьмемо задачі із підручника для 9 класу авторів А. Г. Мерзляк, В. Б. Полонський, М. С. Якір «Аглгебра».(номер в дужках)
Задача 3. (556) Костюм коштував 600 грн. Після того як ціну було знижено двічі, він став коштувати 432 грн., причому відсоток зниження вдруге був у 2 рази більшим, ніж першого разу. На скільки відсотків кожного разу знижувалася ціна?
Розв'язання:
Для спрощення обчислень позначимо
X – перша знижка;
X/2 – друга знижка;
Щоб відшукати невідому X складаємо рівняння
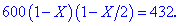
Спрощуємо, та зводимо до квадратного рівняння
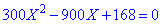
та розв'язуємо
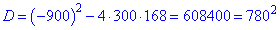
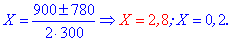
Перший розв'язок не має фізичного змісту, другий враховуємо при обчисленнях. Значення 0,2 відповідає зниженню на 0,2*100%=20% після першої знижки, та X/2 =10% після другої знижки.
Задача 4. (557) Певний товар коштував 200 грн. Спочатку його ціну підвищили на кілька відсотків, а потім знизили на стільки ж відсотків, після чого вартість його стала 192 грн. На скільки відсотків кожного разу відбувалася зміна ціни товару?
Розв'язання:
Оскільки відсотки однакові, то позначаємо зміну ціни товару через X.
На основі умови задачі отримаємо рівняння
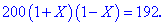
Його спрощення приведе до розв'язування рівняння
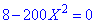
звідки корені набудуть значень
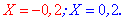
Перша значення відкидаємо, воно міняє суть задачі (спочатку маємо зниження, а потім ріст відсотків, що суперечить умові). Друге при перерахунку становитиме 0,2*100%=20% відсотків.
Задача 5. (558) Вкладник поклав у банк 4000 грн. За перший рік йому нараховано певний відсоток річних, а другого року банківський відсоток збільшено на 4%. На кінець другого року на рахунку стало 4664 грн. Скільки відсотків становила банківська ставка у перший рік?
Розв'язання:
Позначимо через X – збільшення вкладу в перший рік, тоді
X+4/100%=X+0,04
нарахування у другий рік.
За умовою задачі складаємо рівняння для визначення невідомої X
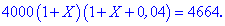
Після спрощень отримаємо квадратне рівняння вигляду
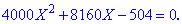
Обчислюємо дискримінант
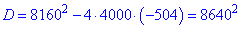
та корені рівняння
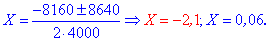
Перший корінь відкидаємо, другий відповідає ставці у 6% річних.
Задача 6. (564) У посудині 12 кг кислоти. Частину кислоти відлили і долили до попереднього рівня водою. Потім знову відлили стільки ж, як і першого разу, і долили водою до попереднього рівня. Скільки літрів рідини відливали щоразу, якщо в результаті отримали 25-відсотковий розчин кислоти?
Розв'язання:
Позначимо через X – частину кислоти,яку відливали.
Після першого разу її залишилося 12-X, а процентний вміст кислоти
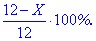
Після другої спроби вміст кислоти у посудині становив
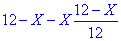 .
.
Розвівши водою до 12 кг, процентний вміст складав 25%. Складаємо рівняння
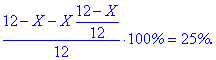
Спрощуємо відсотки та позбуваємося знаменників
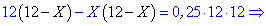
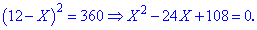
Розв'язуємо квадратне рівняння
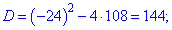
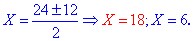
Умові задачі задовільняє другий розв'язок, а це значить, що кожного разу відливали 6 кг рідини.
На цьому знайомство із складними відсотками завершується. На практиці Вам зустрінуться як прості так і складні завдання. При проблемах із обчислення складних відсотків звертайтеся до нас, ми допоможемо Вам у вирішенні задач.


