Найпростіші системи рівнянь (СР), які містять два лінійні рівняння з двома невідомими будуть результатом обчислень складніших СР, серед них звідні до квадратних та ті, що вимагають введення заміни змінних. Завдяки заміні переходимо до простих СР, методика обчислення яких зводиться до додавання рівнянь або підстановки. Уважно перегляньте готові відповіді до прикладів та як їх оформляти, їх підібрано з курсу ЗНО підготовки.
Приклад 20.25 Установити відповідність між системами рівнянь (1–4) та першими компонентами x0 розв'язків (x0;y0) цих систем (А–Д).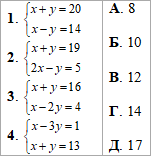
Усі системи рівнянь розв'яжемо методом додавання.

Приклад 20.29 Розв'язати систему рівнянь {2x+5y=12;3x-4y=-5}. У відповідь записати найбільшу суму x0+y0, де (x0;y0) - розв'язок системи.
Обчислення: Розв'яжемо задану систему методом додавання:
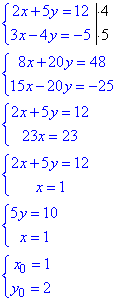
Звідси (1;2) - розв'язок , тоді x0+y0=1+2=3 – сума компонентів розв'язку системи.
Відповідь: 3.
Завдання у збірнику для ЗНО підготовки з номерами за 30 одні з найважчих. Тут вони вчать Вас як заміна змінних дозволяє спростити систему рівнянь та у швидкий спосіб обчислити її.
Приклад 20.31 Розв'язати систему рівнянь {x+y=7;x2+y2=25}. У відповідь записати найбільшу суму розв'язків системи x0+y0.
Обчислення: Перше рівняння описує пряму, друге коло з центром в початку координат. Виразимо з першого рівняння одну змінну через іншу та підставимо у друге
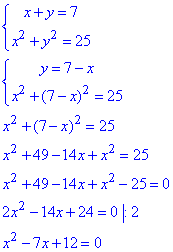
За теоремою Вієта маємо:
x1=3 і x2=4.
Тоді y1=4 і y2=3.
Значення (3;4) і (4;3) - є розв'язками системи рівнянь,
x0+y0=4+3=7 - сума.
Відповідь: 7.
Приклад 20.32 Розв'язати систему рівнянь
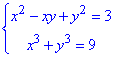
У відповідь записати найбільшу суму x0+y0, де (x0;y0) - розв'язок системи.
Обчислення: Дане рівняння ви не зможете розв'язати, якщо не знаєте формул скороченого множення, а саме як розписати суму кубів. Все решта зводиться до вираження однієї змінної через іншу та перетворення одного з рівнянь до квадратного р-ня
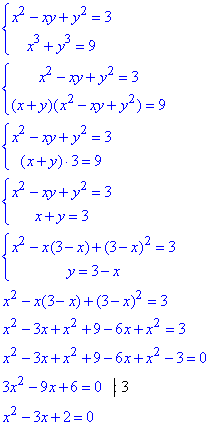
За теоремою Вієта отримаємо:
x1=1 і x2=2.
Тоді y1=2 і y2=1.
(1;2) і (2;1) - розв'язки заданої системи рівнянь є симетричними, тому їх суми рівні:
x0+y0=1+2=3.
Відповідь: 3.
Приклад 20.34 Розв'язати систему рівнянь
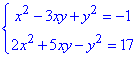
У відповідь записати найбільше значення x із розв'язків системи.
Обчислення: Маємо систему із двох рівнянь другого порядку відносно двох невідомих. Додамо обидва рівняння і запишемо як друге рівняння системи:
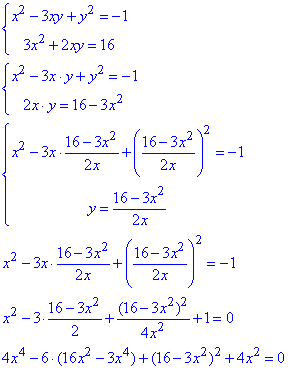
(причому x≠0)
Розкриємо дужки та згрупуємо подібні доданки
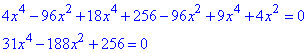
Отримаємо біквадратне рівняння, яке заміною змінних x^2=t≥0 зводимо до квадратного, та розв'язуємо через дискримінант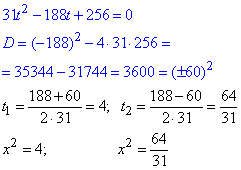
Запишемо чотири "ікси"
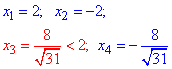
Повернемося до підстановки та обчислюємо "ігрики"
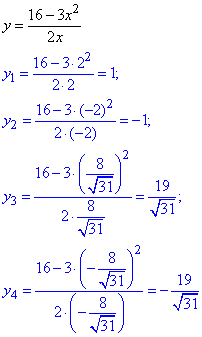
Виписуємо розв'язки системи рівнянь
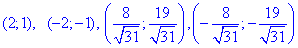
Після порівняння значень, робимо висновок, що x=2 - найбільше значення x із розв'язків системи.
Відповідь: 2.
Приклад 20.35 Розв'язати систему рівнянь
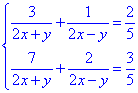
У відповідь записати найбільшу суму x0+y0, де (x0;y0) - розв'язок системи.
Обчислення: Маємо систему рівнянь, змінні в якій містяться в знаменниках дробів. Спершу виписуємо ОДЗ дробових функцій:
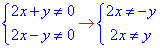
Далі доцільно зробити заміну змінних
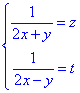
Тоді система рівнянь спроститься до вигляду
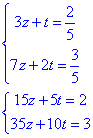
Помножимо перше рівняння на -2 і додамо обидва рівняння:
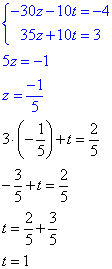
Повернемося до заміни та знайдемо x, y:
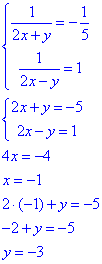
Звідси, (-1;-3) - єдиний розв'язок системи, тому сума компонент і буде найбільшою сумою:
x0+y0=-1+(-3)=-4.
Відповідь: -4.
Приклад 20.37 Розв'язати систему рівнянь
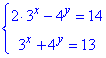
У відповідь записати найбільшу суму x0+y0, де (x0;y0) - розв'язок системи.
Обчислення: Систему показникових рівнянь розв'яжемо за допомогою заміни {3^x=t,4^y=z}, причому t>0,z>0.
З врахуванням заміни, матимемо
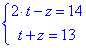
Додамо обидва рівняння:
3t=27, t=9. 9+z=13, z=4.
Повернемося до заміни та знайдемо x, y:
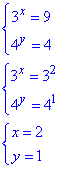
Звідси, (2;1) - єдиний розв'язок системи рівнянь, тому x0+y0=2+1=3 - його сума.
Відповідь: 3.
Приклад 20.39 Розв'язати систему рівнянь
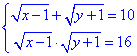
У відповідь записати найбільшу суму x0+y0, де (x0;y0) - розв'язок системи.
Обчислення: ОДЗ коренів квадратних:
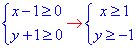
Для спрощення розрахунків вводимо заміну змінних:
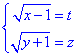
причому
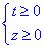
Прийдемо до СР, яку зводимо до лінійного та квадратного рівнянь відносно змінних.
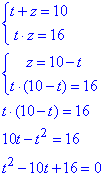
За теоремою Вієта знаходимо корені
t1=2 і t2=8.
Тоді z1=8 і z2=2.
Повернемося до заміни та знайдемо x, y:
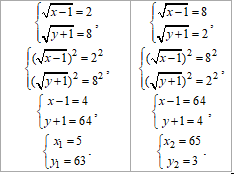
(5;63), (65;3) - розв'язки системи рівнянь, обчислюємо найбільшу суму:
x0+y0=5+63=65+3=68.
Відповідь: 68.
Приклад 20.41 Розв'язати систему рівнянь
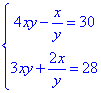
У відповідь записати найбільшу суму x0+y0, де (x0;y0) - розв'язок системи.
Обчислення: Знаменники в дробах не повинні перетворюватись в нуль, звідси умова на ОДЗ: y≠0.
Робимо заміну: {xy=t; x/y=z}, тоді
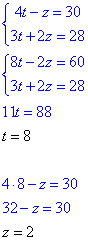
Повернемося до заміни {xy=t; x/y=z} та знайдемо x, y:
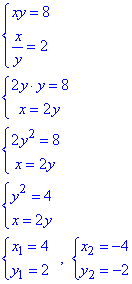
(4;2) і (-4;-2) - розв'язки системи рівнянь, обчислюємо суму компонентів
x0+y0=4+2=6.
Відповідь: 6.
Приклад 20.42 Розв'язати систему рівнянь
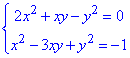
У відповідь записати найбільшу суму x0+y0, де (x0;y0) - розв'язок системи.
Обчислення: Додамо обидва рівняння і запишемо як друге рівняння системи, його розпишемо згрупувавши подібні доданки:
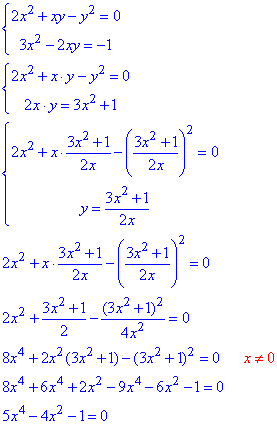
Отримаємо біквадратне рівняння, яке заміною x^2=t>0 зводимо до квадратного
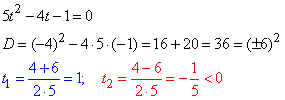
Повертаємося до заміни
x^2=1.
Тоді x1=1, x2=-1.
Знаходимо "ігрик"
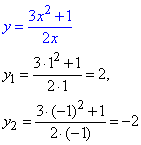
(1;2), (-1;-2) - розв'язки системи рівнянь, перше зі значень вибираємо, щоб отримати найбільшу суму
x0+y0=1+2=3.
Відповідь: 3.
Повірте, що спеціально завдання важкими ми не підбирали. Серед них лише відсортовані та окремо виділені логарифмічні СР, системи рівнянь з модулями та з параметром будуть проаналізовані на наступному уроці. Такі завдання реально можуть чекати Вас на ЗНО тестах та при навчанні у ВУЗ-ах і їх мета всього-навсього первірити, як Ви засвоїли шкільний матеріал та наскільки добре володієте знаннями на практиці.


