де
Комплексні числа називаються спряженими, якщо їх дійсні частини збігаються, а уявні протилежні знаком, тобто, якщо ![]() , то спряжене до нього є
, то спряжене до нього є ![]() .
.
Два комплексні числа називаються рівними, якщо рівні їхні дійсні частини та коефіцієнти при уявних частинах:
![]()
ДІЇ НАД КОМПЛЕКСНИМИ ЧИСЛАМИ, ЗАДАНИМИ В АЛГЕБРАЇЧНІЙ ФОРМІ
Нехай задано два комплексних числа ![]() та
та ![]() .
.
1. Додавання:
![]()
Наприклад, сума двох компексних чисел -1+4i та 3-7i за формулою рівна
![]()
2. Віднімання:
Різницю двох комплексних чисел знаходимо за правилом
![]()
наприклад, віднімемо наступні два числа 3+5i, 1-4i
![]()
3. Множення:
Правило добутку двох комплексних чисел має наступний запис
![]()
Наприклад, помножио число 2+5i на 3+i
![]()
4. Ділення:
Операція ділення досить подібна до позбуття ірраціональності в знаменнику. При діленні чисельник і знаменник потрібно помножити на спряжений вираз до дільника ![]()
![]()
В результаті комплексна частина в знаменнику занулиться і отримаємо класичну формулу комплексного числа.
Наприклад, поділимо 4+5i на 3+2i
![]()
Піднесення уявної частини числа до степеня з натуральним показником ![]() :
:
![]() , якщо
, якщо ![]() ділиться на 4 без остачі;
ділиться на 4 без остачі;
![]() , якщо
, якщо ![]() ділиться на 4 з остачею 1;
ділиться на 4 з остачею 1;
![]() , якщо
, якщо ![]() ділиться на 4 з остачею 2;
ділиться на 4 з остачею 2;
![]() , якщо
, якщо ![]() ділиться на 4 з остачею 3.
ділиться на 4 з остачею 3.
Приклад 1. Обчислити значення виразів
1) ![]()
2) ![]()
3) ![]()
4) ![]()
якщо ![]()
Розв'язок. Основні операції з комплесними числами, це як основа основ даній теорії тому спробуйте розібратися з правилами з першого разу та в майбутньому не мати проблем з обчисленнями.
1) Проведемо додавання та віднімання згідно правил
![]()
![]()
2) Спряженим до числа ![]() буде
буде ![]()
Обчислимо добуток перших двох чисел
![]()
![]()
Обчислимо добуток отриманого числа на ![]()
![]()
![]()
Отже, шуканий добуток буде рівний 65-13i
![]()
3) Виконаємо ділення компексних чисел за формулою
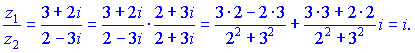
В результаті отримали число, яке має тільки уявну частину.
4) Спочатку підносимо число z3 до квадрату
![]()
Тепер виконаємо ділення
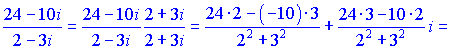
![]()
При обчисленнях будьте уважні і слідкуйте за знаками, як правило, неуважність є причиною більшості помилок при роботі з омплесними числами. Правила піднесення до степеня уявної частини прості і, розв'язавши необхідну кількість подібних прикладів, Ви їх засвоїте без особливих зусиль.
Деякі операції над ними можливо виконувати в спрощеній формі. Нижче будуть наведені правила, які дозволяють швидко обчислювати добуток комплексних чисел, їх частку, піднесення до степеня та знаходження кореня , будь-якого порядку. Правила не надто складні і допоможуть зекономити багато часу на практиці.
1. Множення:
Правило ноження комплексних чисел записаних в тригонометричній формі наступне ![]()
При множенні комплексних чисел їх модулі перемножуються, а аргументи додаються.
2. Ділення:
При діленні комплексних чисел їх модулі діляться, а аргументи віднімаються.
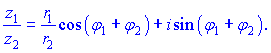
3. Піднесення до степеня:
При піднесенні комплексного числа до степені модуль підносимо до показника, а аргумент на нього множимо
![]()
4. Добування кореня n-го степеня (формула Муавра):
Для обчислення кореня з комплексного числа застосовуємо формулу Муавра-Лапласа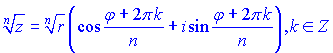
Розглянемо прилад, який в собі містить завдання на піднесення комплексного числа до степеня та добування кореня.
Приклад 1Уважно розгляньте та вивчіть правила піднесення до степеня чисел.
1) Знайти z3, якщо комплексне число задано в тригонометричній формі
![]()
2) Знайти z12, якщо чисо рівне
![]()
3) Знайти корінь квадратний ![]() , якщо z=i.
, якщо z=i.
Розв'язок. Уважно перегляньте та вивчіть методику обчислень!
1) За правилом підносимо до третього степеня
![]()
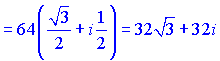
Тут немає чого коментувати, все ілюструє формула.
2) Виконаємо піднесення до дванадцятого степеня
![]()
![]()
Обчислення теж не складні, аргумент 15 градусів дозволяє лего обчислити синус та косинус.
3) Знайдемо корінь квадратний комплексного числа. Подамо число у тригонометричній формі
![]()
За формулою Муавра знаходимо корінь з уявної частини
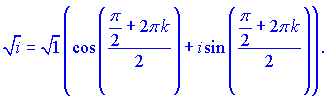
Підставляючи k=0,1, отримаємо два корені
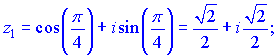
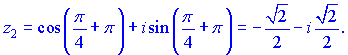
Отримані значення лежать на колі одиничного радіусу з центром в початку координат, відповідно в першій та третій чверті. Варто зазначити, що згідно правила знаходження кількість коренів має бути однакова з показником кореня (степінь 1/2 означає 2 орені числа). Якщо, наприклад маємо корінь ![]() то розв'язків повинно бути n, а в формулі для кореня перебираємо значення k=0,1,...,n-1 і для кожного знаходимо відповідне значення.
то розв'язків повинно бути n, а в формулі для кореня перебираємо значення k=0,1,...,n-1 і для кожного знаходимо відповідне значення.
Розглянемо методику знаходження розв'язку квадратного рівняння з від'ємним дискримінантом. Нехай маємо рівняння вигляду
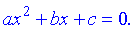
Дискримінант знаходимо за формулою
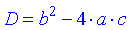
У випадку, коли дискримінант – невід'ємне число 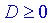 отримуємо два дійсні корені
отримуємо два дійсні корені
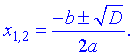
Якщо дискримінант від'ємний D<0, то за властивістю комплексних чисел квадрат уявної частини рівний міну одиниці i2=-1 , тому корені з дискримінанта приймуть значення
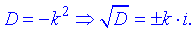
При цьому розв'язок квадратного рівняння з від'ємним дискримінантом тепер існує і його можемо знайти за формулою
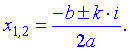
Таким чином, завдяки комплексним числам вдається розв'зати рівняння, які в школі усіх вчили, що не мають коренів. Наведемо розв'язки декількох прикладів.
Приклади 1. Знайти розв'язок квадратного рівняння
(1) 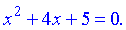
Розв'язок. Обчислюємо дискримінант
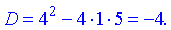
Він від'ємний, тому корені рівняння приймуть комплексні значення
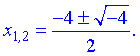
Після спрощень, отримаємо значення
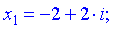
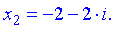
Обчислень, як бачите, небагато і розв'язки отримуємо в досить простий спосіб.
Розглянемо наступне рівняння.
(2) 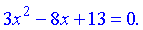
Розв'язок. Обчислюємо дискримінант
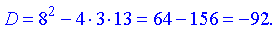
Корінь квадратний з від'ємного дискримінанта прийме значення

Отримане значення підставляємо в формулу коренів
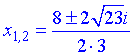
та знаходимо
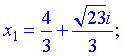
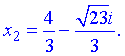
(3) 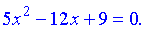
Розв'язок. Дискримінант рівняння як і в попередніх завданнях - від'ємний
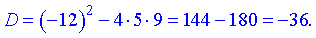
Знайдене значення підставляємо в формулу для обчислення коренів
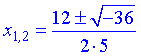
Після простих маніпуляцій отримаємо корені рівняння
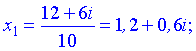
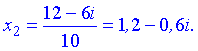
Багатьом з Вас наведені приклади квадратних рівнянь з від'ємним дискримінантом не є складні, а методика розв'язання мабуть знайома. Та сподіваюсь, що серед Вас набереться частина студентів, для яких дана стаття буде корисною та повчальною.
Нехай задана число z0 в комплексній площині чи дійсній, завдання полягає в знаходженні коренів n-го степеня
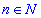 (коренів рівняння zn=z0 ) . Запишемо числа z, z0 в тригонометричній формі
(коренів рівняння zn=z0 ) . Запишемо числа z, z0 в тригонометричній формі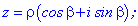
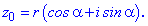
Формула Муавра-Лапласа
За формулою Муавра, маємо наступну залежність між ними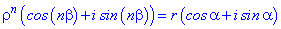 З рівності модулів матимемо матимемо формулу для модулів
З рівності модулів матимемо матимемо формулу для модулів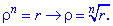 Подібним чином формула Муавра зв'язує аргументи комплексних чисел
Подібним чином формула Муавра зв'язує аргументи комплексних чисел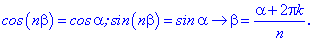 Остаточно, корені рівняння будуть мати вигляд
Остаточно, корені рівняння будуть мати вигляд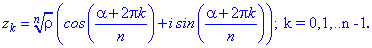
Це і є формула Муавра, яку часто називають формулою Муавра-Лапласа.
При більших значеннях лічильника k=n, ... корені просто будуть повторюватися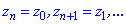 тому параметр змінюється в діапазоні k= 0,..,n-1.
тому параметр змінюється в діапазоні k= 0,..,n-1.
Самі ж корені, а віврніше їх аргументи лежать на колі одиничного радіусу. Достатньо тільки знайти перший, а всі решта отримаємо додаванням кута 2Pi/n.
Розв'яжемо популярні для студентів приклади на відшукання коренів.
Приклад 1. Знайти корені рівняння z3-1=0.
Розв'язання. Перепишемо рівняння у вигляді z3=1 та представимо 1 в тригонометричній формі
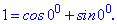
Наступним кроком застосовуємо формулу Муавра
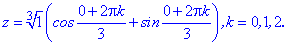
Підстановкою значень k=0,1,2 знаходимо три корені рівняння.
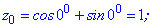
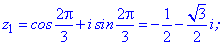
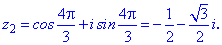
Для спрощення подібних обчислень складемо розрахункову програму в Maple для обчислення і графічної побудови аргументів коренів.
Знаходження коренів комплекного числа в Maple
Для початку обнулимо всі змінні і підключимо пакет роботи з графікою.
> restart;with(plots):
Далі зробимо програмний код універсальним. Для цього для кожного рівняння нам потрібно буде задати лише дійсну частину (a), уявну частину (b) комплексного числа, та корінь якого степеня потрібно знайти (k).
> a:=1; b:=0; k:=3;
Обчислюємо модулі комплексних чисел
> R:=sqrt(a^2+b^2);
> rho=R^(1/k);
Дальше обчислюємо значення аргументу в градусах першого кореня
> alpha:=evalf(arccos(a/R))/3.14*180;
Наступним кроком в циклі обчислюємо корені рівняння, та окремо значення косинусів та синусів кутів.
> for i from 0 to k-1 do
z[i]:=rho*(cos((alpha+2*Pi*i)/k)+I*sin((alpha+2*Pi*i)/k));
x[i]:=cos((alpha+2*Pi*i)/k);
y[i]:=sin((alpha+2*Pi*i)/k) end do;
На основі обчислень, коренями попереднього завдання будуть значення
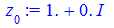
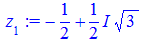
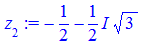
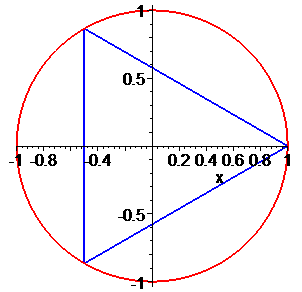
Дальше записуємо код, який відповідає за графічний вивід одиничного кола та многокутника, вершинами якого будуть аргументи коренів. При рівнянні третього порядку отримаємо рівносторонній трикутник, четвертого порядку – квадрат, далі п'ятикутник, шестикутник і т.д.
> Q1:=plot(sqrt(1-x^2), x=-1..1,thickness=2): Q2:=plot(-sqrt(1-x^2), x=-1..1,thickness=2): Q3:=plot([seq([x[m],y[m]],m=0..k-1), [x[0],y[0]]],color=blue,thickness=2):
> display(Q1,Q2,Q3);
Значення аргументів добре ілюструє наступний рисунок. Многокутник відповідає сполученню коренів рівняння.
При необхідності знайдені корені можна округлити
> for i from 0 to k-1 do Z[i]:=evalf(z[i]) end do;
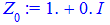
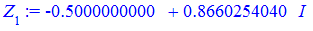
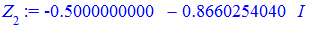
Ось і вся музика.
Приклад 2. Знайти корені рівняння z4+625=0.
Розв'язання. Запишемо рівняння у вигляді 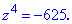 Число в правій стороні рівності (-625) подаємо в тригонометричній формі
Число в правій стороні рівності (-625) подаємо в тригонометричній формі
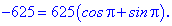
За формулою Муавра корені шукаємо за формулою
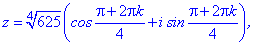
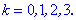
Перебором можливих значень лічильника 0-3 отримаємо
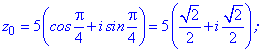
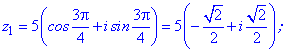
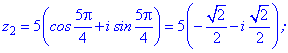
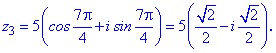
На цьому приклад розв'язано!
Хто має можливість мое вMaple виконуємо перевірку та побудову розв'язків
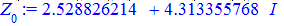
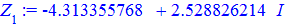
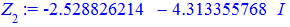
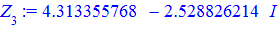
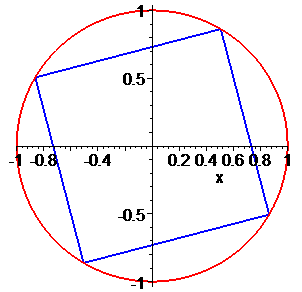
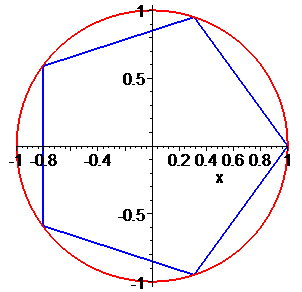
Приклад 3. Розв'язати рівняння z5=1.
Розв'язання. Представимо одиницю в тригонометричній формі
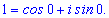
Використовуючи формулу Муавра знаходимо п'ять коренів. Аргументи будуть відрізнятися між собою на кут 2Pi/5=72 градуси
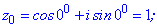
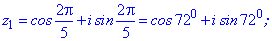
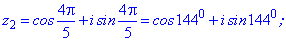
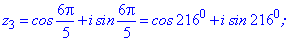
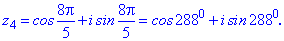
Остаточні значення (з паваючою крапкою) та многокутник отримаємо розрахунками в Maple
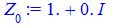
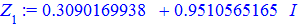
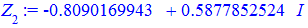
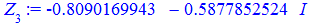
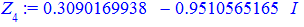
Квадратне рівняння з комплексними коефіцієнтами
Приклад 4. Розв'язати квадратне рівняння з комплексними коефіцієнтами.
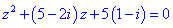
Розв'язання. Розв'язуємо за стандартною схемою для квадратного рівняння. Знаходимо дискримінант рівняння
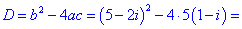
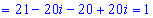
На щастя він приймає дійсне значення – це спрощує обчислення. Знаходимо корені рівняння
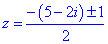
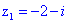 ;
;
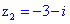
Досить легке в плані розрахунків завдання.
Приклад 5. Розв'язати квадратне рівняння
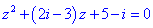
Розв'язання. Обчислюємо дискримінант квадратного рівняння.
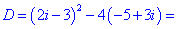
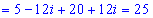
Дальше визначаємо корені за формулою
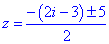
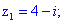
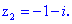
Тут теж повезло з дискримінантом - він виявився дійсним числом.
Приклад 6. Розв'язати комплексне рівняння
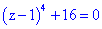
Розв'язання. Хтось подумає "чому комплексне?"
Зараз ми це перевіримо
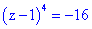
Дійсно комплексне, записуємо константу в тригонометричній формі
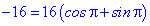
Корені рівняння знаходимо із формули Муавра-Лапласа
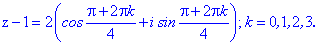
Для кожного із рівнянь отримаємо відповідний розв'язок
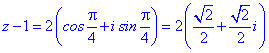
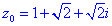
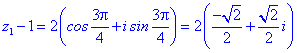
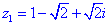
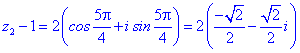
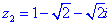
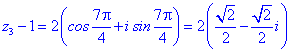
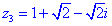
Всі 4 корені належать колу, перший має аргумент 45 градусів, решта 3 зміщені на прямий кут.
Приклад 7. Розв'язати рівняння
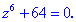
Розв'язання. Тригонометрична форма -64 буде наступною
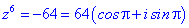
Застосовуємо формулу Муавра для обчислення коренів
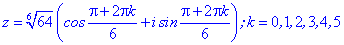
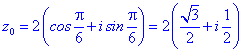
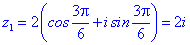
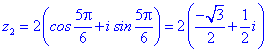
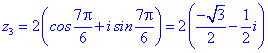
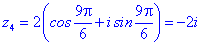
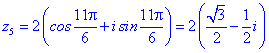
Їх аргументи перевіряємо з допомогою математичного пакету Maple. Графік шестикутника та округлені значення коренів можна переглянути нижче
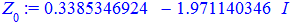
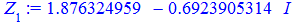
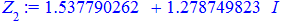
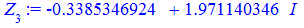
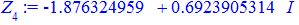
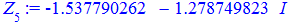
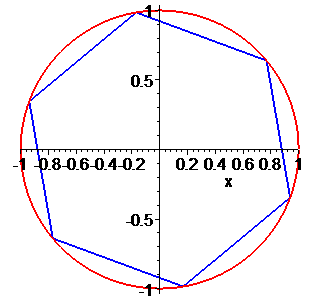
Наведений розрахунковий код для розв'язування комплексних рівнянь в Maple та побудови многокутника аргументів ви можете завантажити за посиланням нижче. З його допомогою можна знаходити корені однотипних рівнянь будь-якого порядку.
]]>Позначимо - кут, який утворює промінь OA з додатним напрямком осі , а через OA=r - довжину променя. Тоді справедливі наступні закономірності
Модулем комплексного числа z називається його довжина в декартовій системі координат, яка визначається за формулою
![]()
Аргумент комплексного числа z визначається так: ![]()
де кут ![]() - визначають із системи рівнянь:
- визначають із системи рівнянь:
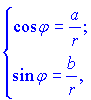
і він належить проміжку [0; 2*Pi].
Для визначення чверті, в якій знаходиться кут, використовують наступні правила
![]() чверть:
чверть: ![]()
![]() чверть:
чверть: ![]()
![]() чверть:
чверть: ![]()
![]() чверть:
чверть: ![]()
Коли ![]() кут приймає значення
кут приймає значення
![]() коли
коли ![]() і
і
![]() у випадках
у випадках ![]()
При ![]() кут приймає значення
кут приймає значення
![]() коли
коли ![]() і
і
![]() у випадках
у випадках ![]()
Запам'ятайте як знаходити кут, це Вам потрібно в першу чергу для обчислень, з іншої сторони підтягнете знання з тригонометрії.
Очевидно, що будь-який розв'язок ![]() системи рівнянь має вигляд
системи рівнянь має вигляд ![]()
Тригонометрична форма комплексного числа
Коротко - це число записане через радіус вектор та кут за форулою
![]()
Два комплексних числа, задані у тригонометричній формі називаються рівними між собою тоді і тільки тоді, коли їх модулі рівні, а аргументи або рівні, або відрізняються на період ![]()
![]()
Розглянемо іька прикладів, щоб закріпити теоретичний матеріал.
Приклад 1. Знайти модуль і аргумент комплексного числа
1) ![]()
2) ![]()
3) ![]()
Розв'язок. Уважно розгляньте та вивчіть схеми наступних перетворень з комплексними числами
1) Знайдемо модуль комплексного числа. Для цього сумуємо квадрати дійсної та уявної чатини числа, після чого добуваємо корінь квадратний
![]()
Кут належить ІV чверті, оскільки a>0, b<0. Знайдемо його значення через тангенс
![]()
Отже, задане комплексне число буде мати наступні модуль і аргумент ![]()
2) Обчислюємо модуль комплексного числа ![]() згідно правила
згідно правила ![]()
Кут ![]() знаходиться в третій чверті, оскільки a<0, b<0. Знайдемо його значення через синус
знаходиться в третій чверті, оскільки a<0, b<0. Знайдемо його значення через синус
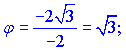
![]()
Заданому комплексному числу має відповідають наступні модуль та аргументу
![]()
3) Модуль числа ![]() знаходимо за формулою
знаходимо за формулою
![]()
Кут ![]() знаходиться в першій чверті, оскільки a>0, b>0.
знаходиться в першій чверті, оскільки a>0, b>0.
Його значення обчислюємо через тангенс
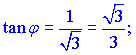
![]()
Шукані величини приймуть значення
![]()
При обчисленнях аргумента комплексного числа через тангенс звертайте увагу на чверть в якій знаходиться кут. Неврахування цього часто приводить до помилок. Обчислення модуля, як правило, простіше і не вимагає особливих знань при вивченні даної теми. Також вивчіть таблицю синусі та осинусів кутів, або хоча б роздрукуйте, щоб мати перед очима при знаходженні аргумену омплексного числа.
Приклади. Знайти розв'язок квадратного рівняння
(1) 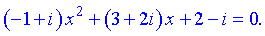
Розв'язок. Знаходимо дискримінант за стандартною формулою
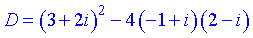
Обчислюємом доданки дискримінанта множенням комплексних чисел
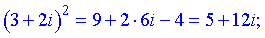
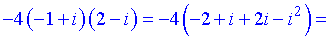
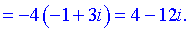
Підставляємо у формулу
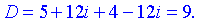
В даному випадку маємо додатній дискримінант з якого можемо взяти дійсний корінь
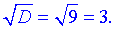
Це дуже спрощує обчислення, оскільки при від'ємному дискримінанті потрібно визначати корені за формулою Муавра.
Знаходимо розв'язок рівняння за формулою
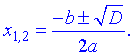
Після підстановки отримаємо корені
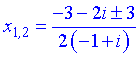
або
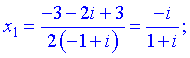
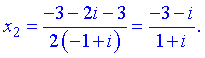
Для спрощення (ділення комплексних чисел), домножуємо чисельник і знаменник на спряжене число до знаменника
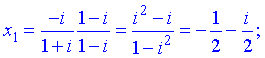
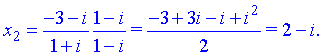
Таким чином наступні значення розв'язків
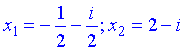
задовільняють вихідне квадратне рівняння.
(2) 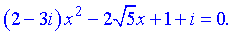
Розв'язок. Дискримінант до квадратичної залежності матиме вигляд
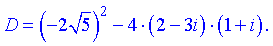
Перший доданок просто знайти
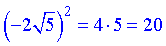
а з другим трохи треба повозитися
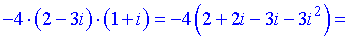
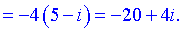
Значення дискримінанту після підстановки буде комплексним
D=20-20+4i=4i.
Для знаходження кореня з дискримінанту застосовуємо формулу Муавра
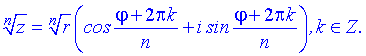
Запишемо отриманий дискримінант в тригонометричній формі
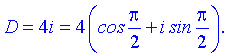
Звідси виписуємо значення модуля та аргументу D
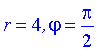
та підставляємо у формулу коренів
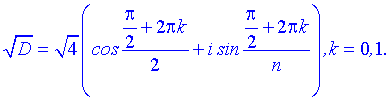
При k=0 матимемо
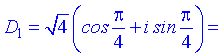
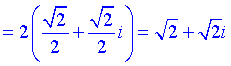
При наступному значенні k=1 отримаємо
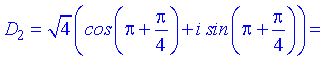
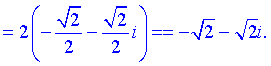
Дані значення відповідають точкам перетину кола з радіусом r=2 та прямої y=x.
Розв'язки квадратного рівняння обчислимо за формулами
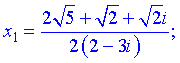
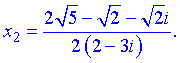
Отримали частки комплексних чисел. Домножимо на спряжене до знаменника і спростимо перший корінь
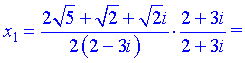
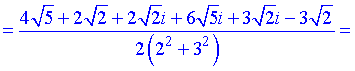
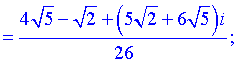
та наступний
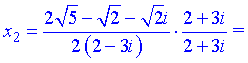
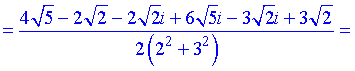
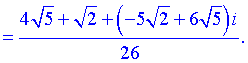
Отримали складні на вигляд розв'язки квадратного рівняння з комплексними коефіцієнтами, однак при розв'язуванні такого сорту прикладів цього не уникнути. В домашніх умовах Вам допоможуть хіба що математичні пакети Maple, Math Cad, Math Lab, Mathematica.
Тепер Ви бачите, наскільки великий об'єм матеріалу з теорії комплексних чисел викладач може перевірити за одну контрольну, задавши Вам усього один приклад!
Тут вам і формула Муавра, множення та ділення комплексних чисел, зведення до тригонометричної форми.
Наведемо методику розв'язання на прикладах, взятих з посібника Тевяшев А.Д., Литвин О.Г., ... "Вища математика в прикладах і задачах." Том 3. Харків 2002 р. Посібники містять багато цікавих задач та їх розв'язки, та рекомендовані Міністерством освіти і науки України для студентів технічних університетів.
Приклади на комплесні числа
Приклад (3.8) Знайти дійсні розв'язки заданих рівнянь
а)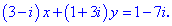
Розв'язання:Розкриємо дужки та перегрупуємо доданки, виділивши дійсну та уявну частину
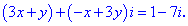
За означенням рівності двох комплексних чисел прирівнюємо дійсну та уявну частини. В результаті отримаємо систему двох лінійних рівнянь
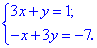
Розв'яжемо отриману систему, для цього з першого рівняння виразимо змінну y та підставимо у друге
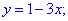
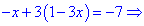
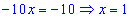
Знайдене значення підставимо в залежність для відшукання y
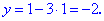
Задане рівняння має розв'язки x=1; y=-2. Схема розв'язування нескладна і після кількох самостійно розв'язаних прикладів Вам добре запам'ятається.
б) 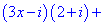
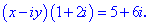
Розв'язання:Перемножимо та згрупуємо подібні доданки
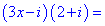
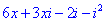
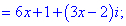
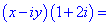
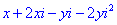
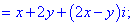
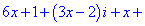
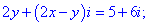
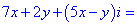
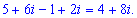
Дане рівняння зводимо до системи лінійних рівнянь
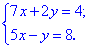
З першого рівняння виражаємо змінну y та підставляємо у друге
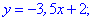
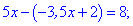
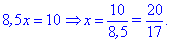
Отримане значення підставляємо в перше рівняння
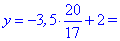
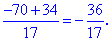
Таким методом отримали наступний розв'язок
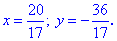
Методика обчислень нескладна і після кількох розглянутих приладів, думаю, Ви зможете повторити обчислення.
Приклад (3.9) Обчислити, за яких дійсних чисел x та y комплексні числа z1 та z2 рівні.
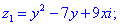
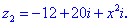
Розв'язання: Прирівнюємо дійсні і уявні частини чисел. В результаті отримаємо два квадратні рівняння
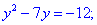
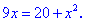
Розв'язуємо кожне з рівнянь для відшукання x та y
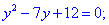
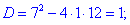
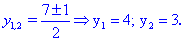
Друге рівняння
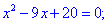
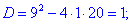
дасть корені 5;4
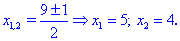
Із знайдених значень отримуємо наступну множину розв'язків
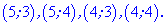
Ось та легко з часом Ви зможете знаходити відповідь до будь-якого завдання, якщо почнети практикувати самостійно.
Приклад (3.10) Визначити, за яких дійсних чисел x та y комплексні числа z1 та z2 спряжені.
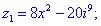
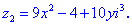
Розв'язання:В даному прикладі потрібно прирівняти дійсну та уявну частину комплексних чисел та врахувати, що для спряжених чисел уявні частини протилежні за знаком. На основі отримаємо
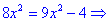
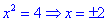
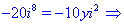
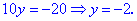
Із знайдених значень сформуємо наступний розв'язок
(-2;2), (2;-2).
При обчисленні подібних прикладів добре вникайте в суть питання: що потрібно знайти ?
В ньому вже міститься підказка - як розв'язати прилад. Решта обчислень пов'язані з властивостями комплексних чисел (множення, піднесення до степеня уявної частини 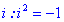 ) і не вимагають складних маніпуляцій. Тож практикуйте з подібними прикладами і поглиблюйте свої знання.
) і не вимагають складних маніпуляцій. Тож практикуйте з подібними прикладами і поглиблюйте свої знання.