Нижче наведені приклади інтегрування, які охоплюють значну частину різноманітних способів знаходження невизначеного інтегралу. Такого типу приклади інтегрування функцій Ви найчастіше побачите на 1,2 курсах навчання з вищої математики. Наведені нижче відповіді одночасно і пояснюють методику взяття інтегралів, і слугують інструкцією з обчислень. Щоб зекономити час та місце самих умов до прикладів ми не виписували.
Приклад 1. Якщо перед інтегралом мали б множником "ікс", то його можна було б внести під диференціал і провести заміну змінних. Однак інтеграл дещо складніший, тому вирази в дужках підносимо до кубу, а далі виконуємо інтегрування кожного з доданків.
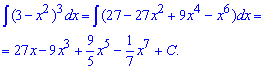
Приклад 2. Задано дробову функцію в знаменнику якої міститься ірраціональність. Щоб її позбутися функцію під коренем позначимо за нову змінну, далі знаходимо її диференціал та підставляємо в інтеграл. Після незначних маніпуляцій з показниками обчислюємо інтеграл, і замість змінної підставляємо виконану заміну.
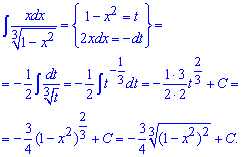
Приклад 3. Хто часто обчислює інтеграли або добре знає теорію інтегралів, то в цьому та подібних завданнях за нову змінну вибирає логарифм. При диференціюванні логарифма отримуємо одиницю розділену на "ікс", що значно спрощує подальше інтегрування. Вкінці не забувайте в прикладах на заміну змінних перейти до початкової змінної "ікс".
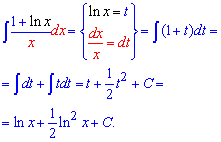
Приклад 4. Виконуємо інтегрування частинами, для цього синус вносимо під диференціал
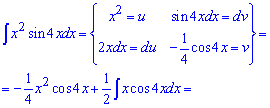
Після першого разу знову отримаємо інтеграл, який обчислюємо інтегруванням частинами.
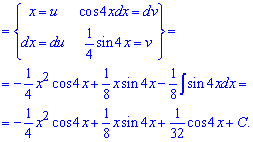
Приклад 5. Маємо завдання під правило інтегрування частинами u*dv. За змінну вибираємо експоненту, а синус вносимо під диференціал.
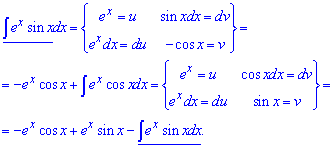
Після повторного інтегрування частинами прийдемо до рекурентної формули, з якої і визначаємо інтеграл.
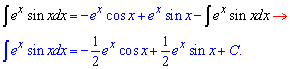
Приклад 6. В цьому інтегралі квадратний тричлен, що стоїть в знаменнику треба звести до суми чи різниці квадратів.
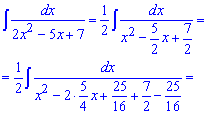
Далі за формулами інтегрування отримаємо арктангенс.
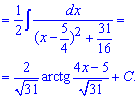
Приклад 7. Інтегрування добутку тригонометричних функцій дається не всім студентам, і тут потрібно враховувати як степені, так і сам вигляд функцій. В цьому прикладі один косинус потрібно внести під диференціал і звести завдання до інтегрування функції від синуса.
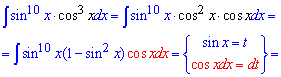
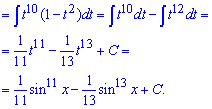
Сам інтеграл не складний і знаходиться за правилом для степеневих функцій.
Приклад 8. Якщо маємо синуси чи косинуси у показниках більших одиниці, то за тригонометричними формулами їх треба порозписувати аж до першого степеня. Далі застосовують формули інтегрування синусів або косинусів.
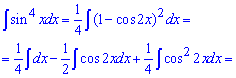
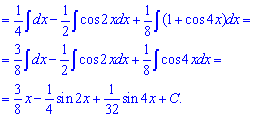
Приклад 9. Щоб знайти інтеграл від дробової функції спершу розділимо чисельник на знаменник, та отриманий в остачі дріб розпишемо на найпростіші дроби. Після цього, використовуючи формули інтегрування, обчислюємо значення кожного з інтегралів.
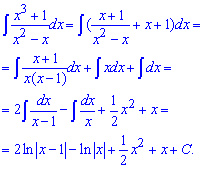
Приклад 10. Маємо інтеграл від дробової функції
![]()
Записуємо її через найпростіші дроби першого та другого типів.
![]()
Далі зводимо дроби під спільний знаменник та з умови рівності чисельників складаємо систему лінійних рівнянь для обчислення невідомих сталих.
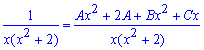
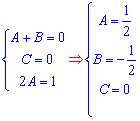
Після її розв'язування повертаємося до дробу, підставляємо сталі та виконуємо інтегрування.
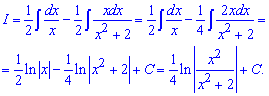
Приклад 11. Маємо інтеграл від дробової ірраціональної функції. Для розкриття ірраціональності виконуємо наступну заміну змінних під інтегралом
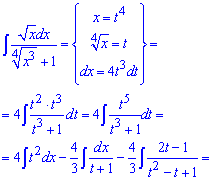
В результаті прийдемо до дробової раціональної функції під інтегралом, яку розписавши на прості дроби легко проінтегрувати
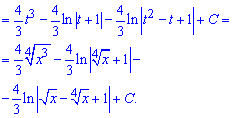
Приклад 12. В цьому завданні для поз буття ірраціональності під інтегралом необхідно використати одну відому хитрість. Вона полягає в тому, що провівши наступну заміну змінних прийдемо до раціональної функції від косинуса.
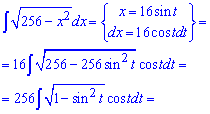
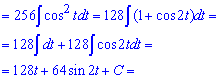
Після інтегрування повертаємося до виконаної заміни і на цьому обчислення можна завершити. Однак, якщо мати під рукою тригонометричні формули то відповідь можна дещо спростити ізаписати в більш компактному вигляді.
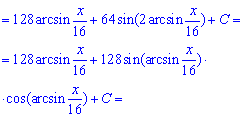
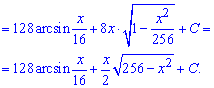
Приклад 13. Маємо в знаменнику раціональну функцію від косинуса і синуса. Такі інтеграли слід знаходити через універсальну тригонометричну заміну t=tg(x/2)
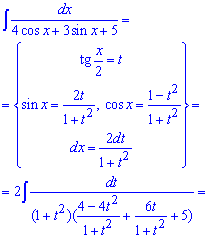
Після підстановки формул синус та косинуса через тангенс половини кута підінтегральна функція перетвориться до дробової, в знаменнику якої матимемо квадратний тричлен. Його зводимо до квадрату виразу, що містить змінну та інтегруємо за правилом для степеневих функцій.
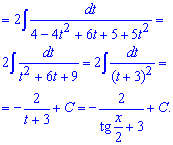
Після інтегрування не забуваємо, що наше t=tg(x/2) і підставляємо його у формулу інтегралу.
На цьому добірка прикладів завершується, більше прикладів Ви знайдете в категорії інтегрування. Для збільшення бази готових інтегралів надсилайте цікаві приклади на Ця електронна адреса захищена від спам-ботів. вам потрібно увімкнути JavaScript, щоб побачити її. або замовляйте у нас розв'язання контрольних робіт та модулів.


