Часто в студентській практиці при інтегруванні зустрічаються приклади, які нескладними маніпуляціями можуть бути зведені для застосування основних формул інтегрування. Таким чином, скориставшись табличним інтегралом, легко обчислити заданий інтеграл.
Розв'яжемо декілька прикладів для засвоєння методу безпосереднього інтегрування.
Приклад 1. Обчислити невизначені інтеграли за таблицею.
а) Розкриваємо дужки, щоб отримати поліном, а далі інтегруємо за відомою формулою
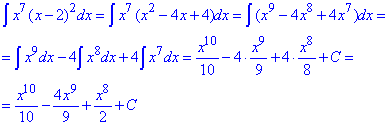
б) Інтеграл замінимо сумою інтегралів, які знаходимо за таблицею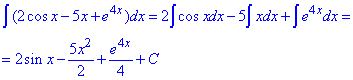
Приклад 2. Знайти інтеграли
а)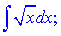 
Розв'язання: Даний інтеграл можна переписати у вигляді
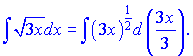
Його знаходимо за формулою степеневих функцій при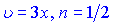 
. Згідно цієї формули отримаємо
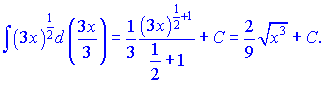
Нічого важкого в роботі з дробовими показниками немає, головне уважність.
б)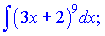 
Розв'язання: Інтеграл обчислюємо за 1 формулою таблиці інтегралів при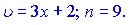 
Внісши дужку під диференціал, обчислення інтегралу дещо спроститься
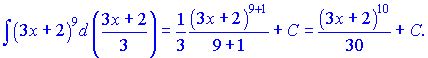
Така техніка в простих випадках дозволяє не проводити заміни змінних.
в)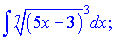 
Розв'язання:Тут перетворюємо корінь до показника та застосовуємо 1 формулу з аблиці інтегралів. Для неї вибирамо
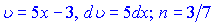
Подальші перетворення дозволяють швидко знайти неозначений інтеграл
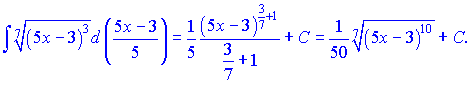
г)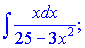 
Розв'язання:Підінтегральна функція може бути зведений до формули (2) таблиці при
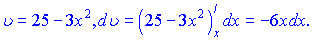
В результаті інтегрування фунції отримаємо
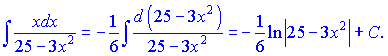
д)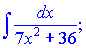 
Розв'язок. Інтеграли такого вигляду знаходимо за формулою (10) . Для цього перетворюємо знаменник дробу та вносимо корінь з семи під диференціал
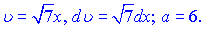
Згідно формул інтегрування неозначений інтеграл рівний арктангенсу
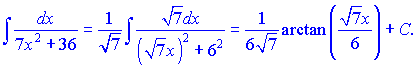
Приклад 1. Обчислити невизначені інтеграли за таблицею.
а) Розкриваємо дужки, щоб отримати поліном, а далі інтегруємо за відомою формулою
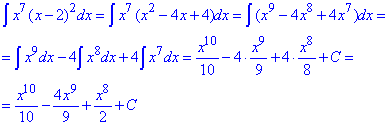
б) Інтеграл замінимо сумою інтегралів, які знаходимо за таблицею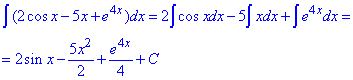
Далі будуть розглянуті завдання, які навчать зводити функції під усі формули таблиці інтеграів. Також Ви познайомитися з рядом методик, без яких складні на вигляд функції в анлітичний спосіб проінтегрувати неможливо. Залишайтеся з нами і навчання математичних дисциплін Вам буде легким і зрозумілим.
