Кратні інтеграли. Індивідуальна робота

Кратні інтеграли являють собою подвійні та потрійні інтеграли. З їх допомогою розв'язують широкий клас задач. За допомогою подвійних інтегралів обчислюють переважно площі фігур на площині, або як їх ще називають - площі криволінійних трапецій. Потрійні інтеграли служать для знаходження об'єму тіл, що утворилися в результаті перетину кількох поверхонь. На практиці вивчають зміну меж інтегрування, що часто дозволяє або спростити або ускладнити обчислення.
Наведені відповіді індивідуальної роботи з вищої математики дозволять Вам легше розуміти теоретичний матеріал та допоможуть при самостійному визначенні меж інтегрування.

ВАРІАНТ – 21

Подвійний інтеграл

ЗАВДАННЯ 1.25 Поміняти порядок інтегрування в подвійному інтегралі:

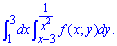
Розв'язання: Випишемо область інтегрування, яка обмежена кривими

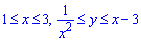
де y=1/x² - гіпербола, y=x-3 - пряма.
Побудуємо графік наведених кривих та заштрихуємо фігуру

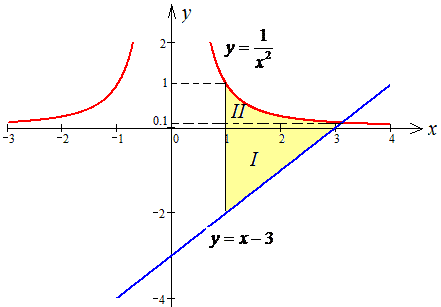
Виразимо отримані функції через змінну y: y=1/x², звідси 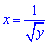, перед радикалом стоїть знак «+» оскільки частина гіперболи (одна з її віток) знаходиться у правій (додатній по x) частині півплощини;
y=x-3, звідси x=y+3.
Точка перетину двох функцій знаходимо з умови x₁=x₂:
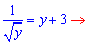1/y=y²+6y+9, 1=y³+6y²+9y, y³+6y²+9y-1=0, звідси наближено y=0,1.
При зміні порядку інтегрування область розбили на дві області: D=D₁+D₂.
На першій частинні змінна проходить від одиниці до прямої, на другій від 1 до гіперболи.
Розставимо межі в кожній області:

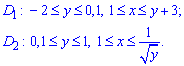
При зміні меж інтегрування отримаємо суму наступних інтегралів

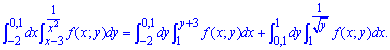
ЗАВДАННЯ 2.6 Знайти площу плоскої фігури, заданої наступними умовами: x²+y²-4x=0, 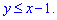. Розв'язання: x²+y²-4x=0, x²+y²-4x+4-4=0, (x-2)²+y²=2² - рівняння кола з центром у точці O(2;0) і радіусом =2.
Умова 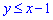- півплощина, що знаходиться нижче прямої y=x-1.
Знайдемо точки перетину графіків заданих функцій x²+y²-4x=0 і y=x-1, для цього можемо друге рівняння (y) підставити в перше
x²+(x-1)²-4x=0, x²+x²-2x+1-4x=0, 2x²-6x+1=0.
При обчисленні отримаємо два корені квадратного рівняння

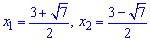
та відповідні їм аргументи

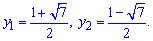
Отож, задану область будемо розбивати на дві області: D=D₁+D₂.

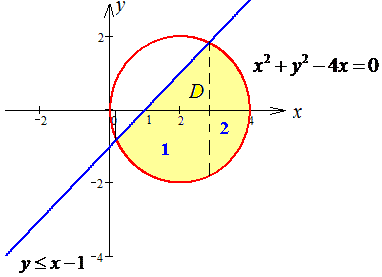
Розставимо межі інтегрування для кожної з областей:

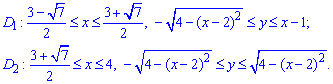
Через подвійний інтеграл обчислюємо площу фігури, обмеженої заданими кривими:

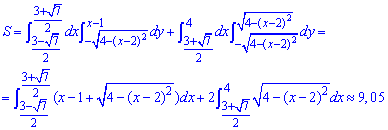
ЗАВДАННЯ 3.14 Обчислити подвійний інтеграл по області D, обмеженій вказаними лініями:
D: y=x3, y=0,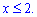
Розв'язання: Побудуємо область інтегрування функції

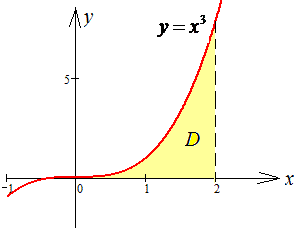
Розставимо межі в заданій області D:

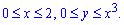
Обчислимо подвійний інтеграл по області D, обмеженій вказаними лініями: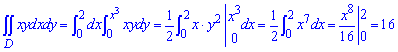

При бажанні, можете поміняти межі інтегрування і переконатися в тому, що результати будуть однаковими. Другий шлях дещо довший, оскільки вилізуть корені, а їх мало хто любить інтегрувати.

ЗАВДАННЯ 4.23 Обчислити подвійний інтеграл, використовуючи полярні координати:

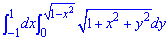
Розв'язання: Побудуємо область інтегрування, яка обмежена кривими

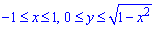
де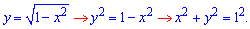
Отримали коло з центром в початку координат O(0;0) і радіусом R=1 (верхня половина).
Перейдемо до полярної системи координат:

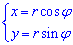
тоді якобіан переходу: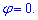
.
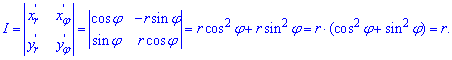Виразимо підінтегральну функцію в полярній системі координат: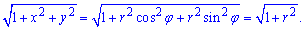

Запишемо межі інтегрування в полярній системі координат:

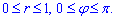
Обчислимо подвійний інтеграл:

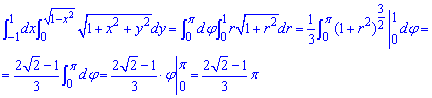
ЗАВДАННЯ 5.24 Обчислити площу області D, обмеженої вказаними лініями:
D: x=4-y², x-y+2=0.
Розв'язання: Знайдемо точку перетину двох графіків x=4-y² і x=y-2:
y-2=4-y², y²+y-6=0, (y-2)(y+3)=0,y₁=-3, y₂=2, x₁=-5,x₂=0.

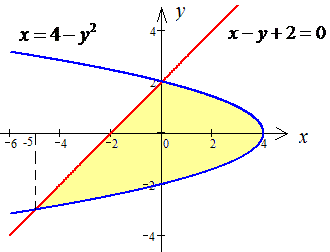
Утворену область D будемо розбивати на дві області: D=D₁+D₂.
Розставимо межі в кожній області:

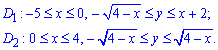
Обчислимо площу області D, обмеженої вказаними лініями:

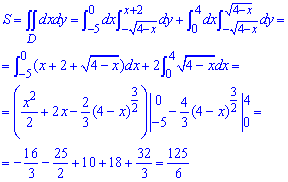
Площа рівна S=20,83(3) од. кв.

ЗАВДАННЯ 6.6 Використовуючи подвійний інтеграл, обчислити, перейшовши до полярних координат, площу плоскої фігури:
Розв'язання: Маємо рівняння фігури у полярній системі координат:

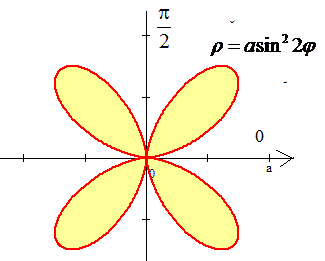
Оскільки задана функція парна, то обчислимо чверть площі і результат помножимо на 4.
Тому межі інтегрування: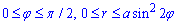
Обчислимо площу плоскої фігури:

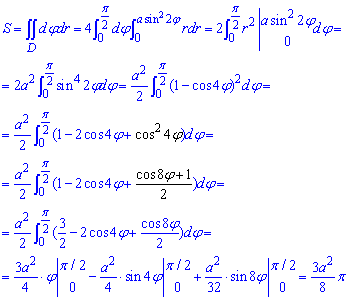
Об'єм тіла, обмеженого поверхнями

ЗАВДАННЯ 7.5 Знайти об'єм тіла, заданого поверхнями, що його обмежують:
x²+y²=4x, x²+y²=8x,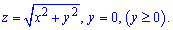
Розв'язання: Перетворимо рівняння першої фігури
x²+y²=4x, x²-4x+4+y²=4, (x-2)²+y²=2²- коловий циліндр, радіусом R=2 і витягнутий вздовж осі Oz. Центр основи (2;0).
Подібні перетворення виконуємо для другого рівняння
x²+y²=8x, x²-8x+16+y²=16, (x-4)²+y²=4²- коловий циліндр, радіусом R=4 витягнутий вздовж осі Oz. Центр основи (4;0).
Підносимо до квадрату функцію 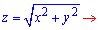z²=x²+y², x²+y²-z²=0 - конус з вершиною у точці O(0;0), витягнутий вздовж осі Oz (верхня частина).
Об'єм тіла, що обмежене заданими поверхнями, будемо шукати при додатних аргументах 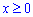і результат помножимо на 2, оскільки задані функції парні відносно осі Ox.

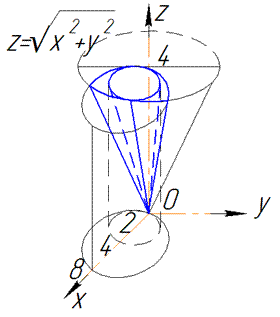
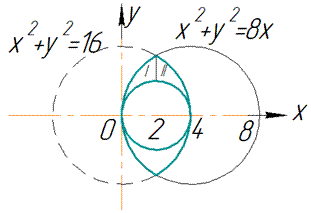
Оскільки утворене тіло не обмежене зверху, то об'єм шукатимемо до площини наприклад z=4, тоді рівняння основи конуса набуде вигляду:
x²+y²=4².
Розставимо межі в заданій області інегрування:

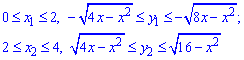
та знайдемо об'єм тіла

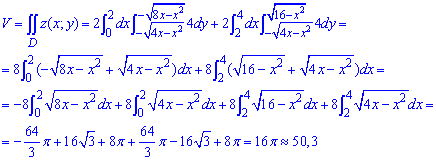
Інтеграл не надто важкий, головне не наробити помилок при підстановці меж та кінцевих спрощеннях.

ЗАВДАННЯ 8.8 Розставити межі інтегрування в потрійному інтегралі 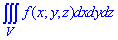, якщо область V обмежена вказаними поверхнями:
V: 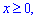y=3x, y=3,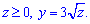
Намалювати область інтегрування.
Розв'язання: Рівняння поверхні в просторі запишемо: z=y²/3 - параболічний циліндр.

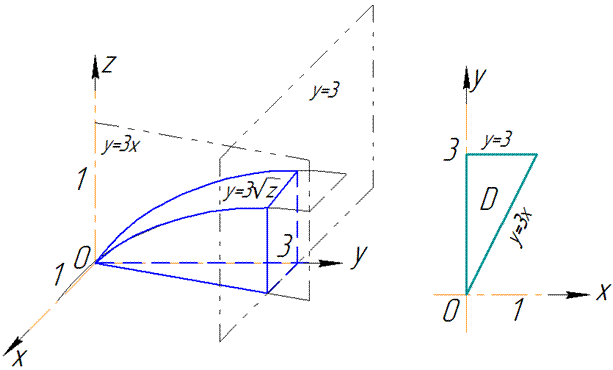
Межі інтегрування розставимо наступним чином:
V: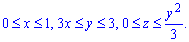
Розставляємо межі в потрійному інтегралі

 

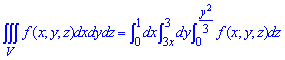
ЗАВДАННЯ 9.1 Обчислити потрійний інтеграл:

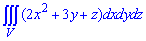
де V: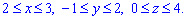
Розв'язання: Задана область V є паралелепіпедом,

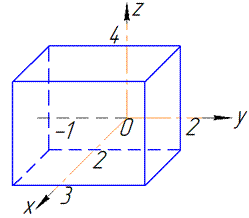
тому без труднощів розставляємо межі інтегрування та знаходимо потрійний інтеграл

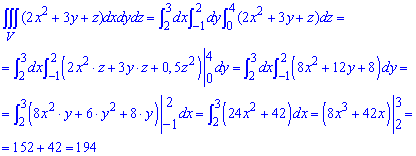
Обчислення не важкі, лише вимагають уважності при підрахунках.

ЗАВДАННЯ 10.21 Використовуючи потрійний інтеграл, обчислити об'єм тіла: де x²+y²=9, z=y², 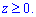. Намалювати область інтегрування.
Розв'язання: Об'єм тіла, утвореного перетином колового x²+y²=9 і параболічного z=y² циліндра будемо обчислювати для четвертини тіла (функції парні), а результат помножимо на 4.
Зобразимо перетин площин та область інтегрування

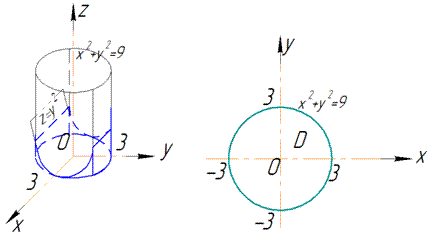
Запишемо межі інтегрування, враховуючи умову і виконаний рисунок:

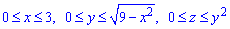
Через потрійний інтеграл знайдемо об'єм тіла: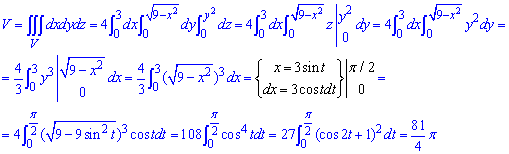

Якщо округлити, то отримаємо об'єм тіла рівний 63,585 од.куб.
Більше прикладів на подвійні та потрійні інтеграли шукайте на сторінках сайту.