ЗНО математика. Задачі на трикутник

Посібник для підготовки до ЗНО тестування з МАТЕМАТИКИ

Підручник для 9-11 класів:
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж

Завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Формат: PDF
Зміст: Посібник містить поради щодо проходження ЗНО з математики та взірці тестових завдань.
Усі задачі однієї теми розміщені в порядку складності.
Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.
Рік випуску: 2010 р.

Тема 29: Трикутники

Далі наведено готові відповіді до 9 з 25 прикладів на трикутники. Завдання містять різноманітні умови на кути, бісектриси, медіани, площу трикутника.
Проаналізувавши пояснення Ви зможете не тільки пригадати матеріал за 7-9 класи школи, але й, можливо, вивчити щось нове, чи познайомитеся з простішою методикою обчислень.
Перегляньте відповіді, які допомогли в підготовці до ЗНО тестів не одному випуску школярів.

Задача 29.17 У трикутнику ABC BM– медіана, <AMB=α, <MBC=β, BM=m.
Визначити сторону AB.

Обчислення: Розглянемо трикутник ABC:

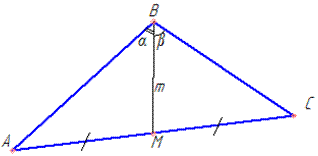
За умовою маємо

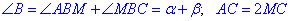
оскільки BM– медіана.
За теоремою синусів складемо відношення і запишемо sin(<C):Б

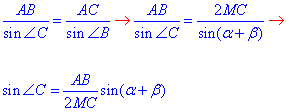
Розглянемо трикутник MBC:
маємо за умовою <MBC=β; BM=m.
За теоремою синусів складемо відношення і запишемо sin(<C):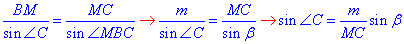

Прирівняємо отримані вирази для знаходження sin(<C) (в обох трик.):

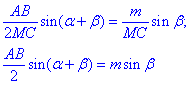
звідси визначаємо невідому сторону трикутника

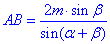
Відповідь: – Д.

Задача 29.18 Два трикутники подібні.
Сторони одного з них дорівнюють 7 см, 12 см і 16 см, а сторони іншого – 40 см, 30 см та x см.
Знайти x.

Обчислення: У подібних трикутників відповідні сторони пропорційні.
Оскільки маємо пропорцію

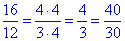
то 12 см і 30 см,
16 см і 40 см – відповідні сторони, тому
16/7=40/x або 16:7=40:x.
Отримали пропорцію:
16•x=40•7
звідси
x=40•7/16=17,5 см.
Відповідь: 17,5 см – Б.

Задача 29.19 У трикутнику ABC відрізок DE з кінцями на сторонах AB і BC паралельний до сторони AC.
Відомі площі трикутників S_DBE=4см², S_DEC=5см² , DE=7 см.
Знайти довжину AC.

Обчислення: Спершу виконуємо побудову трикутника за умовою задачі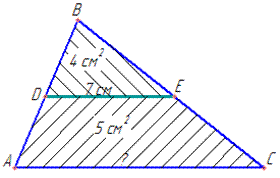
Розглянемо трикутники ABC і DBE: у них <B спільний і <A=<DBE, <B+<DBE як відповідні кути при паралельних прямих AC і DE.
Звіди випливає, що трикутники ABC і DBE подібні (за трьома кутами).
Площі трикутників рівні
S_DBE=4 см² і S_ABC= S_DBE+ S_DEC=4+5=9 см2.
Складемо відношення:

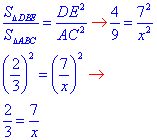
Отримали пропорцію 2:3=7:x.
Розв'яжемо її (добуток крайніх членів = добутку середніх):
2x=7•3,
2x=21,
x=21:2=10,5 см.
Це і є довжина шуканої сторони трикутника.
Відповідь: 10,5 см – Г.

Задача 29.20 S(α) – площа трикутника з даними сторонами a і b та змінним кутом α між ними.
Який з наведених графіків може бути графіком функції S(α)?

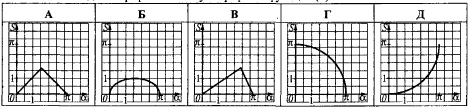
Обчислення: Оскільки площа трикутника через кут виражається формулою S(α) =12•ab•sin(α), то графіком функції є синусоїда на проміжку (0;Pi).
Аналізуємо рисунки А-Д та під Б знаходимо графік синусоїди.
Відповідь: Б.

Задача 29.21 S(h) – площа трикутника з даною стороною a і змінною висотою h, проведеною до неї.
Який з наведених графіків може бути графіком функції S(h)?

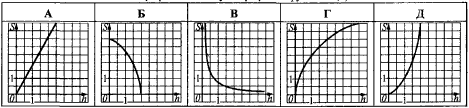
Обчислення: Оскільки площа трикутника через висоту рівна S(h)=1/2•a•h, то графіком функції є пряма.
Єдини вірним графіком, що містить пряму є 1-А.
Відповідь: А.

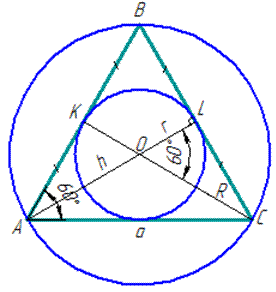
Задача 29.22 Установити відповідність між елементами (1–4) рівностороннього трикутника зі стороною a та їхніми величинами (А–Д).

1. Висота
2. Радіус вписаного кола
3. Кут між медіанами
4. Радіус описаного кола

Обчислення: Побудуємо рівносторонній трикутнник з вписаним та описаним колом.
Внутрішні кути рівні 60 градусів

Знайдемо площу рівностороннього трикутника за формулою:

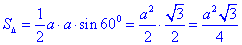
Обчислимо периметр P_Δ і півпериметр p_Δ правильного трикутника:
Периметр: PΔ=a+a+a=3a, тоді півпериметр: pΔ=3a/2.
Висота h рівностороннього трикутника:
S=1/2•a•h, звідси

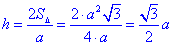
1 – Б.

Радіус вписаного в рівносторонній трикутник кола r знаходимо за формулою:

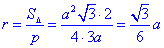
2 – А.

Радіус описаного кола R рівний:

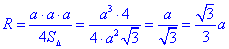
4 – Д.

Кут між медіанами.
У рівностороннього трикутника медіани є одночасно і висотами, і бісектрисами.
Тому кут між медіанами, буде рівним одному з внутрішніх кутів рівностороннього трикутника, тобто 60 градусів.
3 – Г.

Задача 29.23 Установити відповідність між коефіцієнтами подібності (1–4) двох трикутників і відношенням їх площ (А–Д).
1. k1=2
2. k2=3
3. k3=4
4. k4=5

А. 25
Б. 9
В. 16
Г. 36
Д. 4

Обчислення: Відношення площ подібних трикутників дорівнює квадрату коефіцієнта подібності, тобто k^2=A1/A2,
оскільки коефіцієнт подібності k є відношенням лінійних розмірів подібних трикутників.
Звідси отримаємо наступні відповіді:
1 – Д.
2 – Б.
3 – В.
4 – А.

Задача 29.24 Установити відповідність між довжинами сторін (1–4), які лежать проти кута 30 градусів у прямокутних трикутниках, і довжинами діаметрів (А–Д), описаних навколо трикутників кіл. 1. 2 см
2. 4 см
3. 10 см
4. 15 см

А. 8
Б. 20
В. 4
Г. 10
Д. 30
Обчислення: Побудуємо прямокутний трикутник вписаний у коло
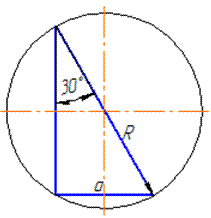За теоремою синусів запишемо рівність:

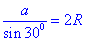
Так як D=2R і sin(30^o)=1/2, то звідси отримаємо рівність D=2a.
Отож, маємо відповіді:
1 – В,
2 – А,
3 – Б,
4 – Д.

Задача 29.25 Установити відповідність між сторонами трикутників (1–4) та їх площами (А–Д).
1. 4 см, 5 см, 3 см
2. 8 см, 10 см, 6 см
3. 16 см, 20 см, 12 см
4. 12 см, 15 см, 9 см

А. 96 см²
Б. 48 см²
В. 6 см²
Г. 54 см²
Д. 24 см²
Обчислення: Взагалі, якщо відомо три сторони трикутника a, b і c, то його площу обчислюють за формулою Герона:

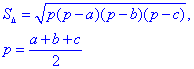
Але помічаємо, що задані трикутники є прямокутними, тому їх площу можна обчислити за спрощеною формулою S=a•b/2, де a і b - катети прямокутного трикутника.
1. 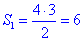см² – В.
2. 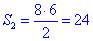см² – Д.

3. 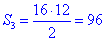см², – А.
4. 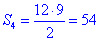см² – Г.

Взяті у формулі значення сторін a і b є катетами відповідних трикутників,
а третя сторона c – їх гіпотенуза.
Це легко можна перевірити за теоремою Піфагора: a^2+b^2=c^2.

На цьому пояснення до 25 задач завершені, далі розберемо тестові приклади на прямокутні трикутники, трапеції та інші фігури.