Задачі на конуси розглядають в 10-11 класі на практичних з геометрії. Також при проходженні ЗНО на Вас чекатимуть завдання на конуси, серед яких багато на твірну конуса. За означенням, твірною називають відрізок, що сполучає вершину конуса з краєм основи – кола. Варіантів задач на знаходження твірної конуса є досить багато як в шкільній програми так і на просторах інтернету.
Далі наведемо кілька готових відповідей до ЗНО тестів, які передбачають або знаходження твірної конуса, або за відомою твірною виведення формули висоти, площі чи кута нахилу твірної до основи.
Задача 39.1 Діаметр основи конуса 8 см, а його висота 3 см. Знайти твірну конуса.
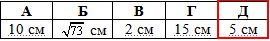
Розв'язання: Маємо конус з висотою H=SO=3 см, в основі якого лежить круг з діаметром D=AB=8 см.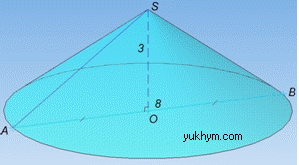
Оскільки конус прямий (інших в школі не розглядаємо), то вершина конуса S проектується в центр основи – точку O, тому всі твірні конуса рівні.
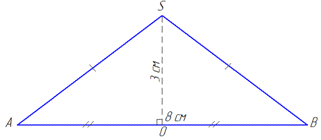
Звідси слідує, що ΔSAB – осьовий переріз конуса – рівнобедрений з основою D=AB – діаметр основи конуса і бічними сторонами l=SA=SB – твірні конуса;
H=SO=3 см – висота, медіана і бісектриса ΔSAB (за властивістю), тому SO⊥AB і R=D/2=OA=OB=4 см – радіус основи конуса.
(В усіх наступних задачах на «конус» перший абзац однаковий (крім числових значень), тому детально про це розписувати не будемо)!
Розглянемо прямокутний трикутник AOS (∠AOS=90), в якому AO=4 см і SO=3 см – катети.
За теоремою Піфагора знайдемо гіпотенузу SA=l – твірну конуса: SA2=AO2+SO2, звідси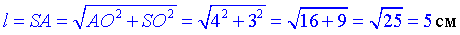 
Отже, l=SA=SB=5 см – довжина твірної конуса.
Відповідь: 5 см – Д.
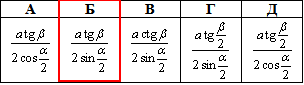
Задача 39.9 Хорду основи конуса, довжина якої a, видно з центра основи під кутом alpha.
Твірна конуса нахилена до площини основи під кутом beta.
Визначити висоту конуса.
Розв'язання: Розглянемо рівнобедрений ΔAOB, у якого AO=B=R – бічні сторони, як радіуси основи конуса, а AB=a – основа, тобто хорда (за умовою задачі).
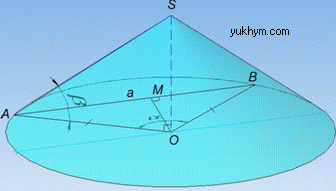
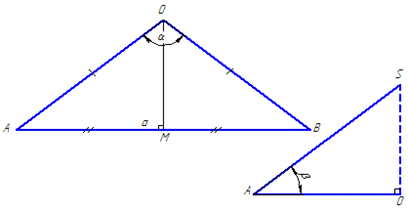
Проведемо висоту OM до основи AB у рівнобедреному ΔAOB (AB⊥OM), тоді OM – медіана і бісектриса ΔAOB (за властивістю), тобто AM=BM=AB/2=a/2.
∠AOB=alpha, оскільки він є центральним кутом вписаним у круг (основу конуса), що опирається на відповідну дугу;
OM – бісектриса, тому ∠AOM=∠BOM=alpha/2.
Розглянемо прямокутний ΔAMO (∠AMO=90), у якого AM=a/2 – протилежний катет до кута ∠AOM=alpha/2.
За означенням синуса гострого кута прямокутного трикутника знайдемо гіпотенузу AO=R:
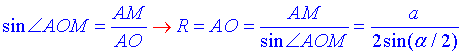
Розглянемо прямокутний ΔSOA (∠SAO=90), у якого
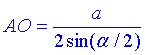– прилеглий катет до кута ∠SAO=beta – кута між твірною SA і площиною основи конуса.
За означенням тангенса гострого кута прямокутного трикутника знайдемо протилежний катет SO=H – висоту конуса:
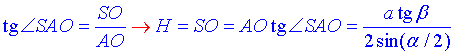, звідси.
Відповідь: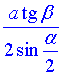 
– Б.
Задача 39.11 Радіуси основ зрізаного конуса дорівнюють 7 см і 15 см, а його твірна – 10 см.
Знайти висоту конуса.
Розв'язання: Маємо зрізаний конус, основами якої є концентричні кола з центрами O та O1, де O1=H – висота зрізаного конуса і радіусами AO=15 см, A1O1=7 см відповідно.
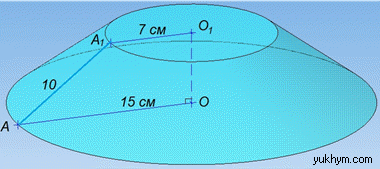
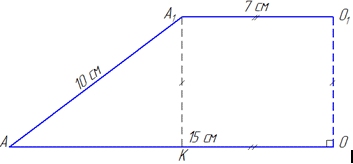
Оскільки висота OO1 перпендикулярна до площин основи зрізаного конуса, то вона перпендикулярна до кожної прямої, що лежить в цих площинах, тому O1⊥AO та OO1⊥A1O1.
Звідси слідує, що чотирикутник AA1O1O – прямокутна трапеція, висота OO1 якої є висотою зрізаного конуса.
Проведемо відрізок A1K=O1O, тобто A1K⊥A.
Тут маємо KO=A1O1=7см, тоді AK=AO-KO=15-7=8 см.
Розглянемо прямокутний трикутник AKA1 (∠AKA1=90), у якого AA1=10 см – гіпотенуза (довжина твірної конуса) та AK=8 см – катет.
За теоремою Піфагора знайдемо катет A1K=O1O – висоту зрізаного конуса:
A1K2=AA12-AK2, звідси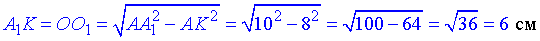 
(Ця задача є аналогічною до задачі 37.31 (треба було слово «піраміда» змінити на «конус»), оскільки конус і піраміда мають багато спільних властивостей і схожих формул для обчислення площі поверхні й об'єму).
Відповідь: 6 см – Г.
Задача 39.12 Два конуси мають однакову площу бічної поверхні.
Знайти відношення площ їх основ, якщо твірна першого конуса утричі більша від твірної другого.
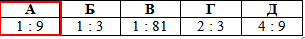
Розв'язання: Площа бічної поверхні конуса обчислюється за формулою:
Sb=πRl,
де R – радіус основи конуса;
l – твірна конуса.
Площа основи конуса:
Soc=πR2.
Маємо два конуси з радіусами основ R1, R2 і твірними l1, l2 відповідно.
За умовою задачі відомо, що l1=3l2 і Sb1=Sb2.
Отже, πR1l1=πR2l2, тому 3R1l1=R2l2.
Отримали співвідношення:
3R1=R2.
Складемо відношення площі основ конуса:
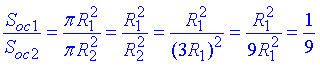
Тобто отримали
.
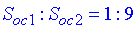Відповідь: 1:9 – А.
Задача 39.15 Відношення площі основи конуса до площі осьового перерізу дорівнює π.
Знайти кут нахилу твірної до основи.
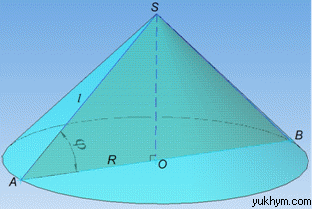
Розв'язання: Площа основи конуса обчислюється за формулою:
Soc=πR2, де R=AO=BO – радіус основи конуса;
l=SA=SB – твірна конуса.
Площа осьового перерізу – ΔSAB:
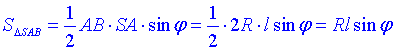
(про осьовий переріз дивись І абзац задачі 39.1), де phi – кут між твірною і діаметром конуса – кут нахилу твірної до площини основи конуса.
За умовою задачі:
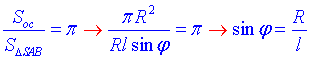
але за означенням косинуса гострого кута прямокутного ΔAOS (∠AOS=90), у якого SA=l – гіпотенуза і AO=R – прилеглий катет до кута ∠SAO=phi маємо:
cos(phi)=R/l, звідси cos(phi)=sin(phi).
В межах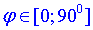 
отримаємо, що phi=45, бо cos(45)=sin(45) (детальніше про тригонометричні рівняння у розділі 18).
Отже, phi=45 – кут нахилу твірної до основи.
Відповідь: 45 – В.
Задача 39.21 Радіуси основ зрізаного конуса дорівнюють R і r, а твірна – l.
Знайти твірну повного конуса, від якого відокремлений зрізаний конус.
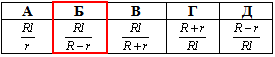
Розв'язання:Маємо зрізаний конус та відокремлений від нього «малий» конус з радіусом основи r=A1O1.
Разом вони складають повний конус з радіусом основи R=AO.
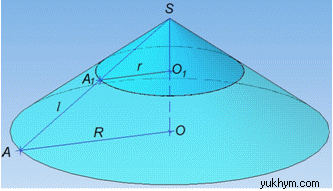
Висота повного конуса SO є сумою висот зрізаного OO1 та «малого» SO1 конусів;
твірна повного конуса SA є сумою твірних зрізаного l=AA1 та «малого» SA1 конусів.
Це доводиться на основі того, що конус утворюється обертанням прямокутного ΔSAO навколо катета SO.
Розглянемо прямокутні трикутники SAO і SA1O1, для яких гострий кут ASO є спільним, тобто ∠ASO=∠A1SO1.
Звідси слідує, що ΔSAO і ΔSA1O1 подібні, а значить їх відповідні лінійні розміри пропорційні:
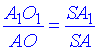
оскільки SA=SA1+AA1, то SA1=SA-AA1, звідси SA1=SA-l.
Отже
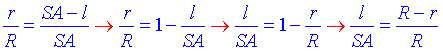
звідси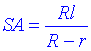 
– довжина твірної повного конуса.
Відповідь: – Б.
Як Ви могли переконатися, обчислення наведених завдань вимагає хороших знань з теорії трикутників та їх властивостей.
Решта формул Вас навчали, коли розглядали на практичних конуси.
Далі будуть не менш цікаві задачі з поясненнями на конуси, вписані та описані навколо пірамід, сфер, циліндрів.
