Прямокутний трикутник. Підготовка до ЗНО

Посібник для підготовки до зовнішнього незалежного тестування з МАТЕМАТИКИ

Підручник для 9-11 класів:
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж

Завантажити (скачати) відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).  Формат: PDF
Зміст: Посібник містить поради щодо проходження ЗНО з математики та взірці тестових завдань. Усі задачі однієї теми розміщені в порядку складності.
Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.

Рік випуску: 2010 р.

Тема 30: Прямокутний трикутник 

Основні формули та співвідношення пов'язані з прямокутним трикутником наведені в посібнику для підготовки до ЗНО. 
Його Ви можете завантажити (без реєстрації) та готуватись по ньому до тестування
Далі будуть наведені готові відповіді до задач, які оформлені по аналогії з відповідями наведеними в збірнику завдань. 

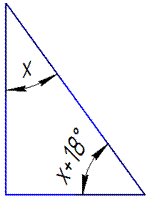
Завдання 30.1 Один з гострих кутів прямокутного трикутника на 180 більший від іншого. Знайти більший з цих кутів.

Обчислення: Перш ніж переходити до розрахунків в геометричних задачах візьміть за правило, скрізь де це можливо, виконувати схематичну побудову.
Точність тут не важлива, головне позначити на трикутнику, що є відомо? та що потрібно знайти?

Далі йдуть пояснення,як оформляти відповіді та обчислювати (взято із шкільної програми).
Нехай x - градусна міра одного гострого кута прямокутного трикутника.
Тоді x+18 - градусна міра іншого гострого кута прямокутного трикутника.
Сума гострих кутів прямокутного трикутника дорівнює 90⁰.
Звідси, x+(x+18)=90⁰.
Розв'яжемо отримане рівняння:
2x+18=90,
2x=90-18=72,
x=72:2=36.
36+18=54 - градусна міра більшого гострого кута прям. трикутника.
Відповідь: Г.

Завдання 30.2 Катети прямокутного трикутника дорівнюють a і a (a>b).
Визначити довжину медіани, проведеної до меншого катета.

Обчислення: У прямокутному трикутнику ABC (<C=90) катет AC=b менший.

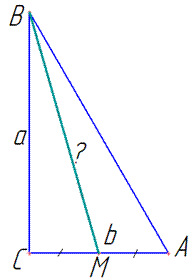
За означенням медіана BM ділить протилежну сторону навпіл, тобто CM=AC/2=b/2.
Розглянемо прямокутний трикутник MBC (<C=90).
У нього відомі два катети:
BC=a і CM=b/2.
Знайдемо гіпотенузу BM.
За теоремою Піфагора маємо:

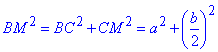
звідси отримаємо

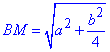
Це і є довжина медіани BM у прямокутному трикутнику ABC.
Відповідь: – Д.

Завдання 30.3 Катет прямокутного трикутника дорівнює 12 см, а медіана, що проведена до нього, дорівнює 8 см.
Знайти інший катет трикутника.

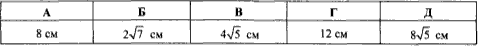
Обчислення: У прямокутному трикутнику ABC (<C=90) катет AC=12 см.

За означенням медіана BM=8 см ділить протилежну сторону навпіл, тобто CM=AC/2=6 см.
Розглянемо прямокутний трикутник MBC (<C=90).
У нього відомі перший катет CM=6 см і гіпотенуза BM=8 см.
Знайдемо другий катет BC.
За теоремою Піфагора маємо:
BC^2=BM^2-CM^2=8^2-6^2, звідси отримаємо
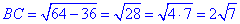см.
В такий спосіб ми знайшли  довжину другого катета BC у прямокутному трикутнику ABC.
Відповідь: 2sqrt(7) см – Б.

Завдання 30.4 Один із катетів і гіпотенуза прямокутного трикутника відповідно дорівнюють 5 см і 13 см.
Знайти площу трикутника.

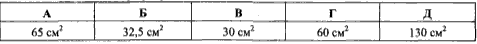
Обчислення: Нехай a=5 см перший катет, а c=13 см гіпотенуза прямокутного трикутника.

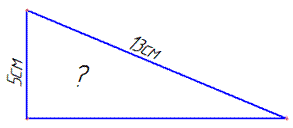
Тоді за теоремою Піфагора знайдемо другий катет b:
b^2=c^2-a^2, тобто b^2=13^2-5^2, звідси
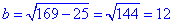см.
Площа прямокутного трикутника обчислюється за формулою пів добутку катетів:
S=ab/2, де a і b - катети прямокутного трикутника.
Підставляємо в формулу
S=5•12/2=5•6=30 см².
Відповідь: 30 см² – В.

Завдання 30.5 Катети прямокутного трикутника дорівнюють 60 см і 80 см.
Знайти висоту трикутника, проведену до гіпотенузи.

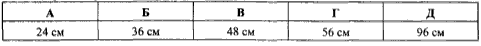
Обчислення: Нехай a=60 см і b=80 см – катети прямокутного трикутника, c - гіпотенуза і h_c - висота трикутника, проведена до гіпотенузи c.

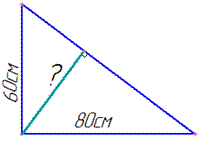
За теоремою Піфагора знайдемо гіпотенузу c:
c^2=a^2+b^2, тобто c^2=60^2+80^2=10000, звідси c=100 см.
Знайдемо площу прямокутного трикутника:
S=ab/2=60•80/2=2400 см².
Але площу довільного трикутника можна обчислити за формулою: (пів добуток сторони трикутника і висоти проведеної до цієї сторони)

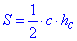
тобто 2400=1/2•100•h_c, звідси маємо h_c=2400•2/100=48 см.
Відповідь: 48 см – В.

Завдання 30.6 Катет та гіпотенуза прямокутного трикутника відповідно дорівнюють 10 см і 26 см.
Знайти проекцію цього катета на гіпотенузу.

Обчислення: Нехай a=10 см – катет і c=26 см – гіпотенуза прямокутного трикутника,
h_c - висота трикутника, проведена до гіпотенузи c.
d - проекція катета a на гіпотенузу c.

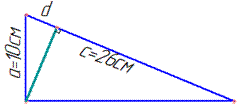
І- спосіб

За теоремою Піфагора знайдемо другий катет b цього ж трикутника:
b^2=c^2-a^2, тобто b^2=26^2-10^2=576, звідси b=24 см.
Знайдемо площу прямокутного трикутника:
S= ab/2=10•24/2=120 см2.
Але площу довільного трикутника можна обчислити за формулою: (пів добуток сторони трикутника і висоти проведеної до цієї сторони)

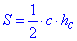
тобто 120=1/2•26•hc , звідси маємо h_c=120•2/26=120/13 см.
Позначимо: d – проекція катета a на гіпотенузу a.
Тоді d^2=a^2-hc^2, звідси

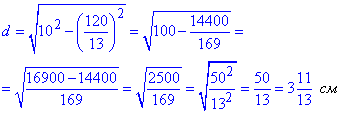
ІІ - спосіб

d - проекція катета a на гіпотенузу c.
За властивістю прямокутного трикутника запишемо: 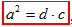, звідси
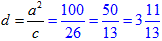см.
Обидва методи обчислень правильні, перший довший в плані часу обчислень, однак формулу з другого способу не всі пам'ятають.
Який варіант з наведених обрати, вибирайте самостійно!
Відповідь: 3 цілих 11/13 см – Д.

Завдання 30.7 Знайти гіпотенузу прямокутного трикутника, у якого висота, проведена до гіпотенузи, дорівнює 6sqrt(3) см, а проекція одного з катетів на гіпотенузу дорівнює 6 см.

Обчислення: Розглянемо прямокутний трикутник: ΔACH (<AHC=90), CH•sqrt(3) см (катет), AH=6 см (катет).

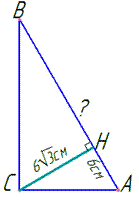
Знайдемо <A:

звідси отримаємо <A=60.
За теоремою Піфагора знайдемо гіпотенузу AC:
AC^2=AH^2+CH^2,
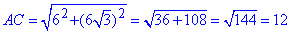см.
Розглянемо прямокутний трикутник:
ΔABC (<ACB=90), AC=12 см (катет), (<A=60).
Знайдемо гіпотенузу AB:

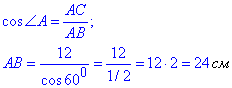
Відповідь: 24 см – В.

Завдання 30.8 Довжина гіпотенузи прямокутного трикутника дорівнює .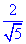
Обчислити площу круга, описаного навколо трикутникуа.

Обчислення: У прямкутному трикутнику радіус описаного кола R дорівнює половині гіпотенузи c, тому .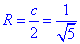

Обчилимо площу круга: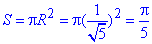
Відповідь: Pi/5 - А.

Завдання 30.9 Один з катетів прямокутного трикутника дорівнює b, а протилежний до нього кут β.
Визначити радіус кола, описаного навколо трикутника.

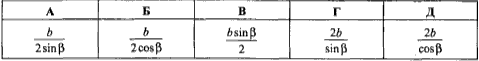
Обчислення: За теоремою синусів: (відношення сторони трикутника до синуса протилежного кута дорівнює радіусу описаного кола, помноженого на 2)
b/sin(β)=2R, звідси отримаємо R=b/( 2sinβ).
Відповідь: b/( 2sinβ) - А.

Завдання 30.10 Гострий кут прямокутного трикутника дорівнює α. Визначити катет, прилеглий до цього кута, якщо радіус кола, вписаного в трикутник, дорівнює r.

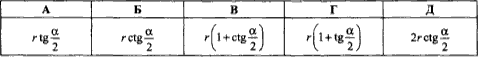
Обчислення: Виконаємо додаткову побудову трикутника до прикладу

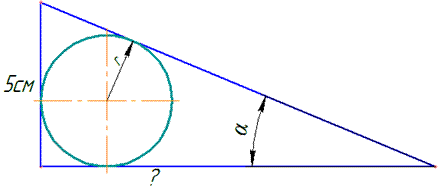
Нехай b=x - прилеглий катет до кута α, тоді a=x•tg(α) - протилежний катет до кута α,
c=x/cos(α) - гіпотенуза цього ж прямокутного трикутника.
Радіус кола, вписаного трикутника визначається за формулою:

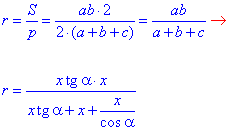
Спростимо вираз у правій частині і знайдемо звідти x:

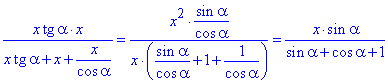
Отже

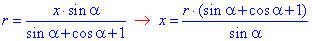
звідси

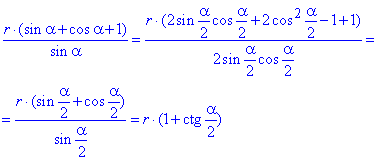
Звідси остаточно маємо x=r(1+ctg(α/2)).
Відповідь: x=r(1+ctg(α/2)) – В.

Завдання 30.11 Катети прямокутного трикутника дорівнюють 5 см і 12см.
Знайти радіус кола, вписаногов трикутник.

Обчислення: Нехай a=5 см і b=12 см – катети прямокутного трикутника. Схематично побудуємо трикутник

За теоремою Піфагора знайдемо гіпотенузу прямокутного трикутника:
c^2=a^2+b^2, звідси
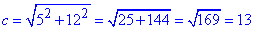см.
Радіус кола, вписаного в трикутник визначається за формулою:
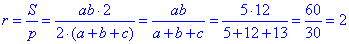см.
Відповідь: 2 см – Б.

Завдання 30.12 У прямокутному трикутнику один з гострих кутів дорівнює α, а висота, що проведена до гіпотенузи, дорівнює h.
Визначити площу трикутника.

Обчислення: Знайдемо довжину прилеглого катета b до кута α:
h/b=sin(α), звідси b=h/sin(α ).

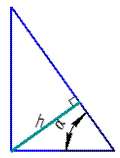
Знайдемо довжину гіпотенузи c:
b/c=cos(α ), тобто

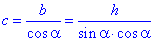
Площу прямокутного трикутника обчислимо за формулою:

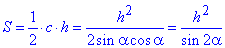
Відповідь: h^2/sin(2α ) – Д.

Завдання 30.13 Гострі кути прямокутного трикутника відносяться як 1:2. Знайти відношення протилежних їм катетів.

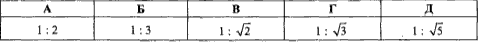
Обчислення: Нехай x один з гострих кутів прямокутного трикутника, тоді 2x - другий гострий кут прямокутного трикутника.

За теоремою про суму кутів прямокутного трикутника маємо:
x+2x=90,
3x=90
звіси x=30 і 2x=60.
Нехай a і b - протилежні катети до кутів 30 і 60 відповідно, тоді за теоремою синусів складемо відношення:
, ,
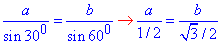або a=b/sqrt(3), звідси a:b=1:sqrt(3).
Відповідь: 1:sqrt(3) – Г.

Завдання 30.14 Один з катетів прямокутного трикутника дорівнює 12 см, а гіпотенуза дорівнює 20 см. Знайти менший з відрізків, на які поділяє гіпотенузу бісектриса прямого кута.

Обчислення: Нехай BC=12 см – катет і AB=20 см – гіпотенуза прямокутного трик.

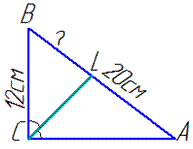
У прямокутному трикутнику ABC (<ACB=90) знайдемо катет AC:

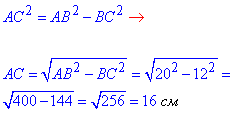
Нехай BL=x, тоді AL=AB-BL=20-x, де BL - бісектриса ΔABC.
Бісектриса трикутника ділить протилежну сторону пропорційно бічним сторонам цього трикутника:
BC/AC=BL/AL, тобто 12/16=x/(20-x), звідси
60-3x=4x,
7x=60,
x=60/7.
Отже, BL=60/7=8 цілих i 4/7 см.
Відповідь: 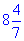см – А.

Завдання 30.15 Бісектриси двох кутів прямокутного трикутника утворюють при перетині кут 79.
Знайти менший гострий кут трикутника.

Обчислення: У прямокутному трикутнику ABC (<ACB=90) BL і CK - бісектриси, які перетинаються в точці O, тоді (за умовою ) <BOK=79.

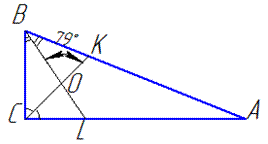
Розглянемо трикутник BOC:
<BCO=<C/2=45,
<BOC=180-<BOK=180-79=101
(кути <BOK і <BOC – суміжні).
За теоремою про суму кутів трикутника BOC знайдемо <CBO:
<CBO=180 –(< BOC+ < BCO)=180-(1071+45)=34.
Оскільки, BL - бісектриса, то <B=2· <CBO=2·34=68.
За теоремою про суму кутів прямокутного трикутника ABC знайдемо <C:
<C =90- <B=90-68=22.
Отже, <C=22 – менший гострий кут ΔABC.
* В цій задачі потрібно ще довести, що бісектриси двох гострих кутів прямокутного трикутника не можуть утворити при перетині кут 79⁰ *.
Це легко виконати маючи всі кути та знаючи, що бісектриса ділить  кут навпіл.
Відповідь: 22⁰ – В.

Завдання 30.16 У прямокутному трикутнику один з гострих кутів дорівнює 27⁰.
Знайти кут між бісектрисою і висотою, проведеними з вершини прямого кута.

Обчислення: У прямокутному трикутнику ABC (<ACB=90) CH - висота,
CL - бісектриса, тому <ACK=<C/2=45.

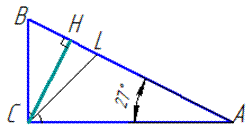
Розглянемо трикутник ACH (<AHC=90), <CAH=27 за умовою.
За теоремою про суму кутів трикутника ACH знайдемо
<ACH: <ACH=180-(<AHC+<CAH)=180-(90+27)=63.
Знайдемо кут <HCL – кут між висотою і бісектрисою трикутника ABC: <HCL=<ACH-<ACL=63-45=18.
Відповідь: 180 – Д.

Решта прикладів на прямокутний трикутник проаналізуємо на наступному уроці.
Якщо Вам сподобалися пояснення до завдань тоді поділіться посиланням в соцмережах та розкажіть про сайт друзям!

Вас може зацікавити:
1. Площа трикутника. Формули
2. Площа та периметр прямокутного трикутника
3. Рівнобедрений трикутник. Знаходження основи, сторін, відрізків
4. Обчислення площі рівнобедреного трикутника. Периметр і площа
5. Задачі на кути трикутника з розв'язками