Далі розберемо готові задачі на правильні чотирикутні піраміди. Завдання одні з найпростіших в темі пірамід, однак і тут прийдеться виводити формули площ та об'ємів. Загалом Ви пригадаєте чимало інформації з геометрії за 10-11 клас, яка одним допоможе в розрахунках. Іншим дасть зрозуміти, що геометрія не така і проста наука. Для її вивчення необхідні добрі знання простих основ: тригонометричних формул синуса, косинуса, теореми Піфагора.
Без потрібних знань викладений тут матеріал буде Вам складним для сприйняття та розуміння.
Ви можете безкоштовно завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 37.2 Правильна чотирикутна піраміда. Площа та об'єм піраміди
Задача 37.5 Висота правильної чотирикутної піраміди дорівнює 8 см, апофема піраміди – 10 см. Знайти у квадратних сантиметрах площу перерізу піраміди, проведеного через середину висоти паралельно до площини основи.
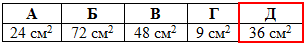
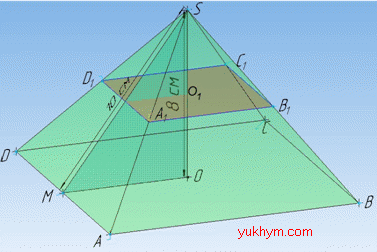
Розв'язання: В основі правильної чотирикутної піраміди SABCD маємо квадрат ABCD.
Проекція вершини правильної піраміди співпадає з центром основи піраміди (в точку перетину діагоналей квадрата), звідси SO=8 см – висота піраміди.
Проведемо відрізок MO⊥AD. Оскільки висота SO піраміди перпендикулярна до площини основи (квадрата ABCD), то вона перпендикулярна до кожної прямої, що належить площині основи, тому SO⊥MO. Проведемо відрізок (похилу) SM. Оскільки MO⊥AD, то за теоремою «про три перпендикуляри» SM⊥AD, звідси SM=10 см – висота бічної грані правильної чотирикутної піраміди – апофема піраміди.
У прямокутному трикутнику SOM (∠SOM=90), у якого SO=8 см – катет, SM=10 см – гіпотенуза знайдемо інший катет MO:
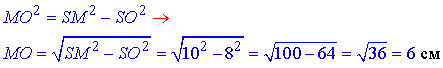
У квадраті MO⊥AD, де точка O – центр квадрата (точка перетину діагоналей), тому (за властивістю квадрата) MO||AB і AB=2MO=12 см (це доводиться на основі того, що MO – середня лінія трикутника ACD).
Площа основи (квадрата ABCD) піраміди:
SABCD=AB2=122=144 см2. За властивістю: площина яка проходить паралельно основі піраміди відтинає подібну піраміду. Маємо правильну чотирикутну піраміду SA1B1C1D1 з висотою SO1=SO/2=8/2=4 см (за умовою задачі) і основою – квадрат A1B1C1D1.
У подібних фігур площі пропорційні до квадратів їх лінійних розмірів, тому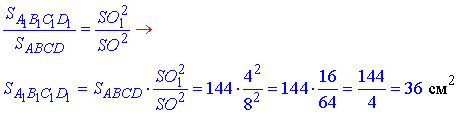 
Відповідь: 36 см2 – Д.
Задача 37.6 Висота та бічне ребро правильної чотирикутної піраміди відповідно дорівнюють 3 см і 5 см. Знайти об'єм піраміди.
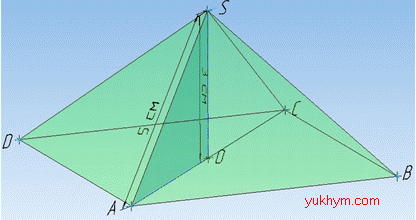
Розв'язання: В загальному випадку об'єм піраміди обчислюють за формулою:
V=1/3•Soc•H, де Soc – площа основи;
H – висота піраміди.
В основі правильної чотирикутної піраміди SABCD лежить квадрат ABCD.
Вершина правильної піраміди проектується в центр основи піраміди, звідси SO=H=3 см – висота піраміди, SA=5 см – бічне ребро піраміди.
Оскільки висота перпендикулярна до площини основи (квадрата ABCD), то вона перпендикулярна до кожної прямої, що лежить в цій площині.
Таким чином SO⊥AO, де AO – половина довжини діагоналі квадрата ABCD.
У прямокутному трикутнику SAO (∠SOA=45), у якого SO=3 см – катет, SA=5 см – гіпотенуза знайдемо інший катет AO:
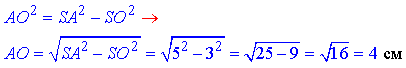
Довжина діагоналі квадрата:
AC=2AO=2•4=8 см.
Площа квадрата ABCD (основи правильної чотирикутної піраміди):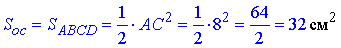 
Далі знаходимо об'єм піраміди:
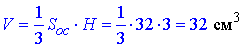
Відповідь: 32 см3 – Д.
ЗНО 2020. Завдання 30. Висота правильної чотирикутної піраміди дорівнює 12 см, апофема - 13 см. Обчисліть об'єм (у см3) цієї піраміди.
Розв'язування: Об'єм піраміди обчислюють за формулою:
В основі правильної чотирикутної піраміди SABCD лежить квадрат ABCD. Виконаємо допоміжну побудову
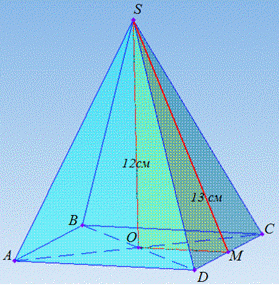
Вершина правильної піраміди проектується в центр основи піраміди (в точку перетину діагоналей квадрата), звідси SO=H=12 см – висота піраміди.
Проведемо відрізок MO⊥CD.
Оскільки висота SO піраміди перпендикулярна до площини основи (квадрата ABCD то вона перпендикулярна до кожної прямої, що належить площині основи, тому SO⊥MO.
Проведемо відрізок (похилу) SM.
Оскільки MO⊥CD, то за теоремою «про три перпендикуляри» SM⊥CD, звідси SM=13 см – висота бічної грані правильної чотирикутної піраміди – апофема піраміди.
У прямокутному трикутнику SOM (∠SOM=90), у якого SO=12 см – катет, SM=13 см – гіпотенуза,
знайдемо інший катет MO:
MO2=SM2-SO2, звідси
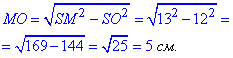
У квадраті MO⊥CD, де точка O – центр квадрата (точка перетину діагоналей), тому (за властивістю квадрата) MO||AD і AD=2MO=2∙5=10 см
(це доводиться на основі того, що MO – середня лінія трикутника ACD).
Обчислимо площу
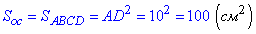
За формулою обчислюємо об'єм піраміди:
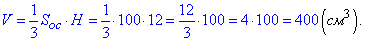
Відповідь: 400.
Задача 37.17 Повна поверхня правильної чотирикутної піраміди дорівнює S. Двогранний кут при ребрі основи – 600. Визначити бічну поверхню піраміди.
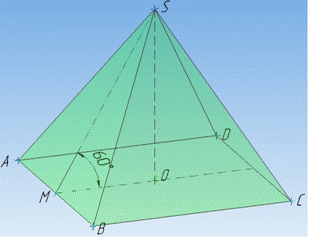
Розв'язання: Маємо правильну чотирикутну піраміду SABCD, в основі якої лежить правильний чотирикутник (квадрат) ABCD.
Нехай довжина сторони квадрата дорівнює a.
Тоді площа основи піраміди (квадрата):
Soc=SABCD=a2.
Висота SO правильної чотирикутної піраміди проектується у центр квадрат ABCD, тобто в точку O перетину діагоналей AC і BD.
З точки O проведемо відрізок MO перпендикулярно до сторони AB, тобто MO⊥AB. За властивістю квадрата:
MO||BC і MO=BC/2=a/2.
Оскільки висота SO перпендикулярна до площини основи (квадрата ABCD), то вона перпендикулярна до кожної прямої, що лежить в цій площині, тому SO⊥MO.
Проведемо відрізок SM. Оскільки MO⊥AB, то за теоремою «про три перпендикуляри» SM⊥AB. Звідси слідує, що ∠SMO=60 – лінійний кут двогранного кута (двогранний кут) при ребрі основі – кут нахилу бічної грані до площини основи.
Розглянемо прямокутний трикутник SOM (∠SOM=90), у якого MO=a/2 – прилеглий катет до ∠SMO=60.
За означенням косинуса гострого кута прямокутного трикутника знайдемо гіпотенузу SM – апофему піраміди:
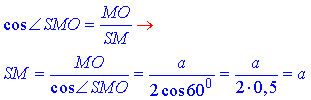
Площа бічної поверхні правильної чотирикутної піраміди: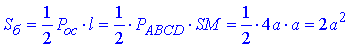 
Площа повної поверхні піраміди:
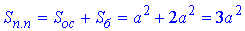
Але за умовою задачі Sпп=S, тому 3a2=S, звідси a2=S/3.
Площа бічної поверхні піраміди:
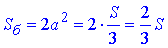Відповідь: 2S/3 – Д.
Задача 37.18 Діагональним перерізом правильної чотирикутної піраміди є прямокутний трикутник, площа якого дорівнює Q. Знайти площу основи піраміди.
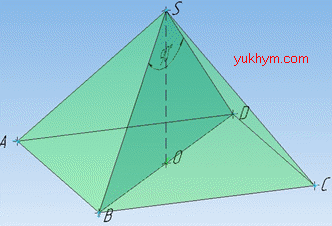
Розв'язання: Маємо правильну чотирикутну піраміду SABCD, в основі якої лежить правильний чотирикутник (квадрат) ABCD.
Нехай довжина сторони квадрата ABCD дорівнює a.
Тоді площа основи піраміди (квадрата):
Soc=SABCD=a2.
Висота SO правильної чотирикутної піраміди проектується у центр квадрат ABCD, тобто в точку O перетину діагоналей AC і BD. Діагоналі квадрата рівні:
AC=BD=a√2 (за теоремою Піфагора із прямокутного ΔBCD).
Діагональним перерізом піраміди є прямокутний трикутник BSD (∠BSD=90) за умовою задачі. Висота SO є одночасно висотою піраміди SABCD і висотою ΔBSD, опущеної з вершини прямого кута.
Оскільки в правильній піраміді всі бічні ребра рівні, то SB=SD, тому ΔBSD – рівнобедрений з основою BD і бічними сторонами SB=SD.
За властивістю кутів рівнобедреного трикутника:
∠SBD=∠SDB=45, тому ∠SDO=∠SDB=45.
Розглянемо прямокутний ΔSOD (∠SOD=90).
Запишемо довжину
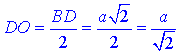– прилеглого катета до кута ∠SDO=45.
Із означення тангенса гострого кута прямокутного трикутника знайдемо SO – висоту піраміди і ΔBSD:
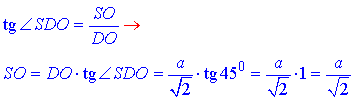
Звідси маємо SO=a/√2.
Далі знаходимо площу трикутника ΔBSD:
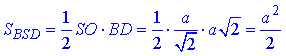
Але за умовою задачі SBSD=Q, тоді a2/2=Q, звідси виражаємо a2=2Q – площа основи.
Відповідь: 2Q – А.
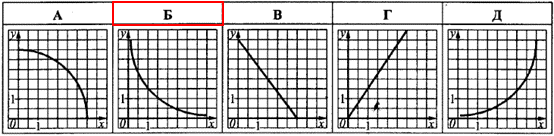
Задача 37.22 S(x) – площа перерізу правильної чотирикутної піраміди, проведеного паралельно до основи на відстані x до неї. Який з наведених графіків може бути графіком функції S(x)?
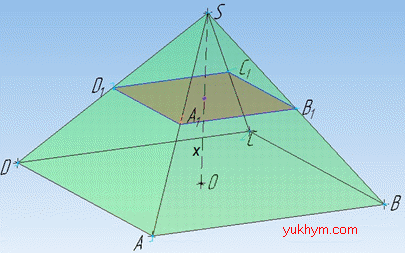
Розв'язання: Маємо правильну чотирикутну піраміду SABCD з висотою SO=H і площею основи (квадрата) SABCD:
SABCD=S.
Площина, яка проходить паралельно основі відтинає подібну піраміду.
Таким чином, маємо піраміду SA1B1C1D1 подібну до даної.
Площа перерізу (квадрату A1B1C1D1) дорівнює S(x), де x – відстань між двома основами пірамід. Тоді висота піраміди дорівнює H-x.
У подібних фігур площі пропорційні до квадратів їх лінійних розмірів: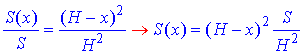 
Отримали квадратичну залежність площі перерізу (квадрата A1B1C1D1) від відстані x між основами подібних пірамід. Чим менша відстань x, тим більша площа перерізу.
Це відповідає графіку на рисунку Б.
Відповідь: Б.
Задача 37.27 Площа діагонального перерізу правильної чотирикутної піраміди дорівнює S і є прямокутним трикутником.
Установити відповідність між площею перерізу (1–4) та площею бічної поверхні (А – Д) піраміди.
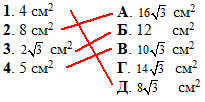
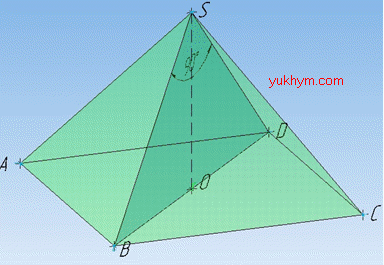
Розв'язання: Маємо правильну чотирикутну піраміду SABCD, в основі якої лежить правильний чотирикутник (квадрат) ABCD.
Нехай довжина сторони квадрата ABCD дорівнює a.
Тоді площа основи піраміди (квадрата):
Soc=SABCD=a2.
Площа бічної поверхні правильної чотирикутної піраміди:
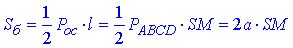
де SM – апофема піраміди (висота бічної грані).
Висота SO правильної чотирикутної піраміди проектується у центр квадрата ABCD, тобто в точку O перетину діагоналей AC і BD.
Діагоналі квадрата рівні:
AC=BD=a√2 (за теоремою Піфагора із прямокутного ΔBCD.
З точки O проведемо відрізок MO перпендикулярно до сторони CD, тобто MO⊥CD.
За властивістю квадрата:
MO||BC і MO=BC/2=a/2.
Оскільки висота SO перпендикулярна до площини основи (квадрата ABCD), то вона перпендикулярна до кожної прямої, що лежить в цій площині, тому SO⊥MO.
Проведемо відрізок SM. Оскільки OM⊥DC, то за теоремою «про три перпендикуляри» SM⊥AD. Діагональним перерізом піраміди є прямокутний трикутник BSD (∠BSD=90) за умовою задачі. Висота SO є одночасно висотою піраміди SABCD і висотою ΔBSD, опущеної з вершини прямого кута.
Оскільки в правильній піраміді всі бічні ребра рівні, то SB=SD, тому ΔBSD – рівнобедрений з основою BD і бічними сторонами SB=SD.
За властивістю кутів рівнобедреного трикутника:
∠SBD=∠SDB=45, тому ∠SDO=∠SDB=45. Розглянемо прямокутний ΔSOD (∠SOD=90), у якого
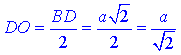– прилеглий катет до ∠SD0=45.
За означенням тангенса гострого кута прямокутного трикутника знайдемо катет SO – висоту піраміди і ΔBSD:
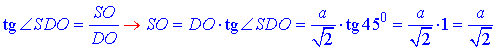
Отже, SO=a/√2.
Розглянемо прямокутний ΔSOM (∠SOM=90), у якого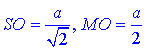 
катети.
За теоремою Піфагора знайдемо гіпотенузу SM – апофему піраміди: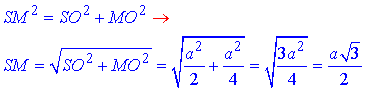 
Площа ΔBSD:
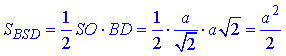
Але за умовою задачі SBSD=S, тоді a2/2=S, звідси a2=2S – площа основи.
Площа бічної поверхні правильної чотирикутної піраміди:
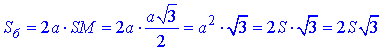
Обчислимо площу бічної поверхні для кожного випадку:
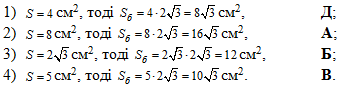
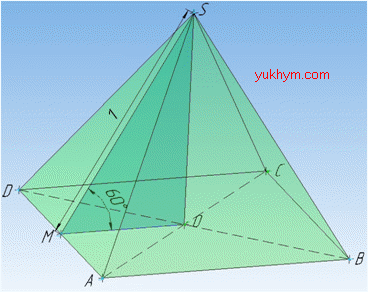
Задача 37.32 Апофема правильної чотирикутної піраміди дорівнює 1 і нахилена до площини основи під кутом 600. Визначити повну поверхню піраміди.
Розв'язання: Площа повної поверхні правильної піраміди:
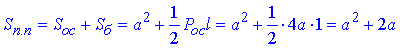
Soc=a2 – площа основи (квадрата ABCD) правильної чотирикутної піраміди;
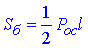– площа бічної поверхні;
Poc – периметр основи;
l=SM=1 – апофема.
Висота SO правильної чотирикутної піраміди проектується у центр квадрата ABCD (зі стороною a), тобто в точку O перетину діагоналей AC і BD.
З точки O проведемо відрізок MO перпендикулярно до сторони AD, тобто MO⊥AD.
За властивістю квадрата:
MO||AB і MO=AB/2=a/2.
Оскільки висота SO перпендикулярна до площини основи (квадрата ABCD), то вона перпендикулярна до кожної прямої, що лежить в цій площині, тому SO⊥MO. Проведемо відрізок SM.
Оскільки MO⊥AD, то за теоремою «про три перпендикуляри» SM⊥AD.
Звідси слідує, що ∠SMO=60 – лінійний кут двогранного кута (двогранний кут) при ребрі основі – кут нахилу бічної грані (апофеми) до площини основи.
Розглянемо прямокутний трикутник SOM (∠SOM=90), у якого SM=1 – гіпотенуза ∠SMO=60.
За означенням косинуса гострого кута прямокутного трикутника знайдемо прилеглий катет MO=a/2 – половину сторони основи:
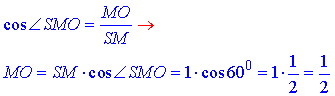
Обчислимо довжину сторони основи (квадрата ABCD):
MO=a/2=1/2, звідси a=1.
Площа повної поверхні правильної піраміди:
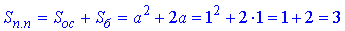
Відповідь: 3.
Задача 37.35 У правильній чотирикутній піраміді відстань від центра основи до бічної грані дорівнює 3. Бічні грані нахилені до основи під кутом 600.
Визначити об'єм піраміди.
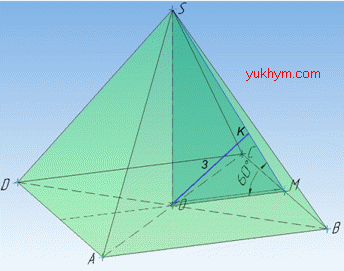
Розв'язання: Об'єм піраміди обчислюється за формулою:
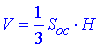
де Soc=SABCD=a2 – площа основи (квадрата ABCD) піраміди SABCD зі стороною a,
H=SO – висота піраміди.
Висота SO правильної чотирикутної піраміди проектується у центр квадрата ABCD (зі стороною a), тобто в точку O перетину діагоналей AC і BD.
З точки O проведемо відрізок MO перпендикулярно до сторони BC, тобто MO⊥BC.
Висота SO перпендикулярна до площини основи (квадрата ABCD), тому вона перпендикулярна до кожної прямої, що лежить в цій площині, SO⊥MO.
Проведемо відрізок SM. Оскільки MO⊥BC, то за теоремою «про три перпендикуляри» SM⊥BC. Звідси слідує, що ∠SMO=60 – лінійний кут двогранного кута (двогранний кут) при ребрі основі – кут нахилу бічної грані (апофеми) до площини основи.
Проведемо відрізок KO=3 – відстань від центра основи до бічної грані, KO⊥SM. Тоді із прямокутного OKM (∠OKM=90) за означенням синуса гострого кута ∠OMK=60 визначаємо сторону OM
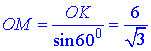
За властивістю квадрата: MO||AB і рівна половині
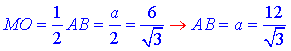
Можамо знайти площу основи піраміди
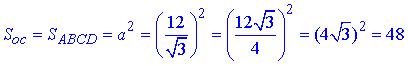
– площа основи (квадрата ABCD).
Розглянемо прямокутний трикутник SOM (∠SOM=90), у якого OM=6/√3 – прилеглий катет до кута (∠SMO=60). За означенням тангенса гострого кута прямокутного трикутника знайдемо протилежний катет SO – висоту піраміди:
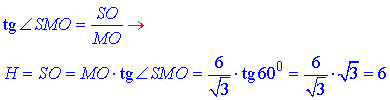
Об'єм піраміди:
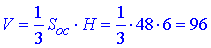
Відповідь: 96.
Всім хто дочитав статтю до кінця дякуємо за терпіння. Матеріалу досить багато, але тут лише частина з 35 готових відповідей.
Далі на Вас чекають задачі на зрізані піраміди та трикутні й чотирикутні, де в основі маємо прямокутник чи відмінні від рівностороньього трикутники.
Ці задвдання в повній мірі допоможуть Вам в підготовці як до практичних з геометрії, так і до можливих вступних тестів.
