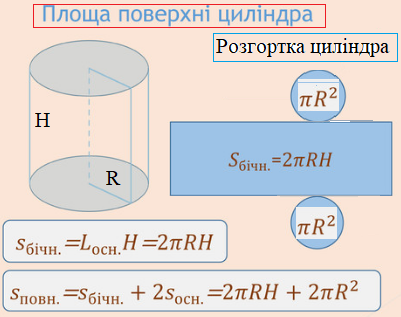
Площа повної поверхні циліндра рівна площі бічної поверхні,яка в розгортці є прямокутником і площі 2 основ циліндра, які є кругами радіуса R.
S(повна)=2πR2+2πRH
Площа бічної поверхні циліндра рівна добутку довжини основи L(осн.)=2πR на висоту цидіндра H:
S(біч.п.)=2πRH.
Площа основи циліндра — S(круга)=πR2.
Схематично все що стосується обчислення площі циліндра наведено на рисунку
Розглянемо готові відповіді до задач на знаходження повної площі та площі бічної поверхні циліндра. Задачі взято із посібника для ЗНО підготовки з математики. Формули, що тут наводяться вчать у 9-11 класі шкільної програми з геометрії, їх наводимо лише в задачах де це має зміст.
38.2 Площа поверхні циліндра
Задача 38.1 Знайти повну поверхню циліндра з радіусом 5 см і висотою 15 см.
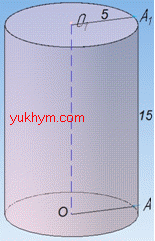
Розв'язання: Маємо циліндр з висотою H=OO1=AA1=15 см, в основі якого лежить круг з радіусом R=OA=O1A1=5 см.
Повну поверхню циліндра (її площу) знаходимо за формулою:
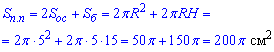
де 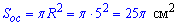 – площа основи циліндра (площа круга);
– площа основи циліндра (площа круга);
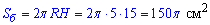 – площа бічної поверхні циліндра.
– площа бічної поверхні циліндра.
Це одні з поширених формул, тому добре запам'ятайте їх.
Відповідь: 200π см2 – Г.
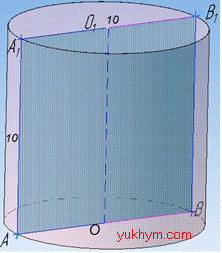
Задача 38.5 Осьовим перерізом циліндра є квадрат зі стороною 10 см.
Знайти площу бічної поверхні циліндра.
Розв'язання: Площа бічної поверхні циліндра обчислюється за формулою:
Sb=2πRH,
де R – радіус (основи) циліндра;
H – висота (довжина твірної) циліндра.
Осьовим перерізом циліндра є квадрат AA1B1B зі стороною 10 см (за умовою задачі), сторони AA1=BB1 якого є твірними циліндра (їх довжина дорівнює висоті H циліндра), тому H=10 см.
Дві інші сторони AB=A1B1=10 см – діаметри основ циліндра.
Вісь OO1 циліндра є віссю квадрата, його кінці ділять діаметр навпіл, тобто AO=OB=A1O=OB1=R=AB/2 см, де R=5 см – радіус циліндра.
Знаходимо площу бічної поверхні циліндра за формулою:
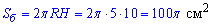
Відповідь: 100π см2 – Г.
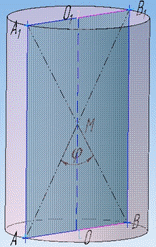
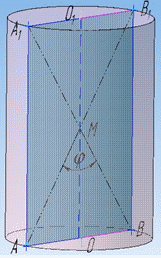
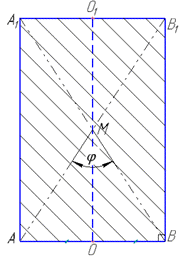
Задача 38.11 Діагоналі осьового перерізу циліндра утворюють при перетині кут phi.
Визначити площу бічної поверхні циліндра, якщо площа його основи дорівнює S.
Розв'язання: Ще раз повторимо, що формула площі бічної поверхні циліндра має вигляд:
Sb=2π•R•H, де R – радіус (основи) циліндра;
H – висота (довжина твірної) циліндра.
В основі циліндра лежить круг, площа якого S (за умовою задачі).
Але площа круга розраховується за формулою:
Soc=π•R2=S, звідси отримаємо залежність
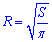 – радіус (основи) циліндра.
– радіус (основи) циліндра.
Осьовим перерізом циліндра є прямокутник AA1B1B.
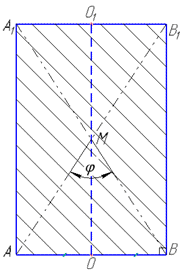
Вісь (висота) циліндра є віссю прямокутника, тобто ділить його на два рівних прямокутники.
Діагоналі AB1 і A1B прямокутника AA1B1B рівні і в точці перетину M діляться навпіл (за властивістю).
Тому ΔAMB – рівнобедрений з основою AB, а MO – висота, медіана і бісектриса, тому справедлива залежність
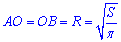
∠OMB=1/2•∠AMB=phi/2, ∠BOM=90.
Розглянемо прямокутний ΔBOM (∠BOM=90), у якого 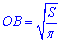 – катет протилежний до кута ∠OMB=phi/2.
– катет протилежний до кута ∠OMB=phi/2.
За означенням тангенса гострого кута прямокутного трикутника знайдемо прилеглий катет OM:
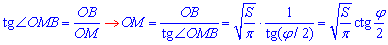
Так як діагоналі AB1 і A1B прямокутника рівні і в точці перетину M діляться навпіл, то ΔAMB і ΔA1MB1 – рівні, звідси знаходимо
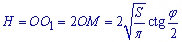 – висоту циліндра.
– висоту циліндра.
Маємо всі складові для обчислення площі бічної поверхні циліндра:
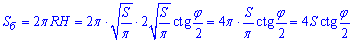
Завдання не з простих, зате отримали корисну для практики компактну формулу бічної поверхні.
Відповідь: 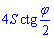 – А.
– А.
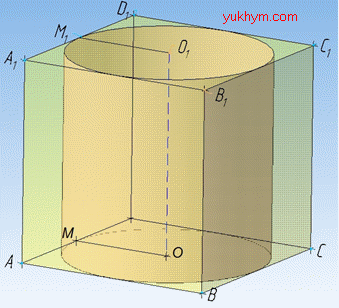
Задача 38.15 У куб, ребро якого дорівнює a, вписано циліндр. Визначити повну поверхню циліндра.
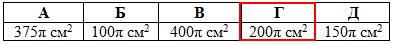
Розв'язання: Знову задано приклад на виведення формул.
Запишемо формулу для знаходження повну поверхні (її площу) циліндра формулою:
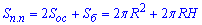
де Soc=πR2 – площа основи циліндра (площа круга);
Sб=2πRH – площа бічної поверхні циліндра.
Циліндр вписаний у призму (циліндр вписаний у куб за умовою), якщо основи циліндра вписані в основу призми (коло вписано в квадрат), а висота циліндра дорівнює висоті призми.
Маємо куб з ребром a (у куба всі ребра рівні). Звідси слідує, що висота циліндра дорівнює ребру куба, тобто H=AA1=…=DD1=OO1=a.
Коло вписано в квадрат, якщо сторони квадрата дотикаються до кола, а центр кола лежить на перетині діагоналей квадрата.
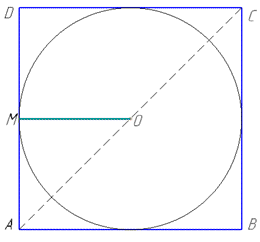
Проведемо відрізок MO перпендикулярно до сторони AD, AC діагональ квадрата ABCD. Оскільки сторона квадрата є дотичною до кола, то MO=R=a/2 (тобто відрізок MO є радіусом кола (циліндра)), а також відрізок MO є середньою лінією ΔADC.
Площа повної поверхні циліндра розписуємо за формулою:
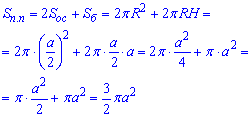
Після групування подібних доданків та сумування отримаємо просту квадратичну залежність площі поверхні циліндра від сторони описаного куба.
Відповідь: 3/2•π•a2 – Б.
Площа бічної поверхні
Задача 38.27 Кут між твірною циліндра і діагоналлю осьового перерізу дорівнює 600, площа основи циліндра дорівнює √3. Визначити площу бічної поверхні циліндра. 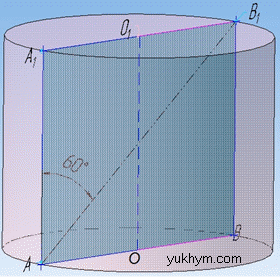
Розв'язання: Формула площі бічної поверхні циліндра:
Sб=2πRH,
площа основи:
Soc=πR2.
Але за умовою задачі основа відома Soc=√3, звідси можемо виразити радіус круга π•R2=√3.
Маємо осьовий переріз циліндра – прямокутник AA1B1,/B зі сторонами AA1=BB1=H (висота) і AB=A1B1=2R (діаметр циліндра), який проходить через вісь OO1 циліндра. ∠A1AB=60 – кут між твірною AA1 циліндра (тобто стороною прямокутника AA1B1B) і діагоналлю AB1 перерізу AA1B1B.
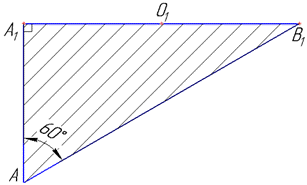
Із прямокутного трикутника AA1B1 (∠AA1B1=90), у якого A1B1=2R – протилежний катет до кута ∠A1AB1=60.
За означенням тангенса гострого кута прямокутного трикутника знайдемо прилеглий катет AA1=H – висоту циліндра:
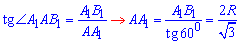
Знаючи висоту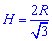 без проблем запишемо формулу площі бічної поверхні циліндра:
без проблем запишемо формулу площі бічної поверхні циліндра:
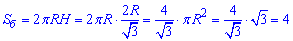
Відповідь: 4.
Задача 38.22 Площа основи циліндра дорівнює S, а діагоналі осьового перерізу утворюють при перетині кут phi. Установити відповідність між величинами S і phi (1–4) та площею бічної поверхні циліндра (А–Д).
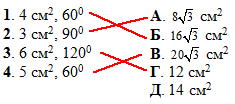
Розв'язання: (Розв'язок цієї задачі дивись у номері 38.11.)
Обчислимо площу бічної поверхні циліндра за знайденою формулою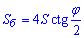 для кожного із тестових випадків:
для кожного із тестових випадків:
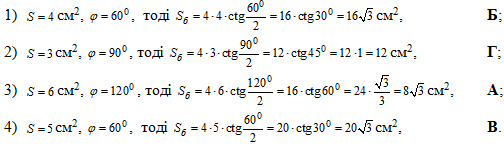
Далі розглянемо обчислення радіуса, висоти циліндра, осьових перерізів і т.д.


