Проаналізуємо готові відповіді до ЗНО тестів на обчислення об'єму конусів, які утворилися в результаті обертання трикутника навколо сторони, ромба навколо діагоналі. Простих прикладів зі шкільної програми за 9-11 клас Ви тут не знайдете, хоча формули та методика розрахунків незмінні. В цій та інших статтях наведені відповіді до понад 40 завдань на конуси.
В умовах задач на конуси відомі геометричні розміри, площі поверхонь чи об'єм. У відповідь потрібно знайти одну з наведених величин через інші, часто потрібно вивести формулу, яку не вивчали у шкільному курсі геометрії, проте не складно отримати з геометричних формул (синус, косинус, тангенс кута, пропорції і т.д.).
Всі ці приклади збагатят Ваші практичні знання та допоможуть на ЗНО тестуванні.
Задача 39.4 Прямокутний трикутник з катетами 3 см і 4 см обертається навколо меншого катета.
Обчислити об'єм утвореного тіла обертання.
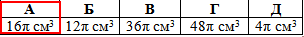
Розв'язання: Маємо прямокутний ΔAOS (∠AOS=90), в якому AO=4 см – більший катет, SO=3 см – менший катет і SA – гіпотенуза.
Тіло, яке утвориться при обертанні прямокутного ΔAOS навколо меншого катета SO називається конусом.
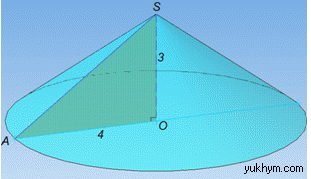
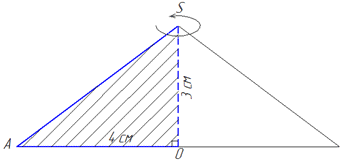
Вісь (висота) конуса – менший катет прямокутного ΔAOS (H=SO=3 см);
радіус основи конуса – більший катет прямокутного ΔAOS (R=AO=4 см), а твірна конуса – гіпотенуза SA прямокутного ΔAOS.
Об'єм конуса обчислюється за формулою:
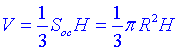, де 
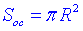– площа основи конуса, площа круга.
Ця формула дуже добре вивчається на практичних в 9-10 класі і доступна у самих простих посібниках по фігурах.
Все що залишається, це підставити вхідні величини та знайти
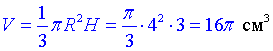– об'єм конуса, утвореного при обертанні прямокутного ΔAOS навколо катета SO=3см.
Відповідь: 16π см3 – А.
Задача 39.18 Сторона основи правильної чотирикутної піраміди дорівнює a.
Бічна грань утворює з площиною основи кут alpha.
Визначити об'єм конуса, вписаного в піраміду.
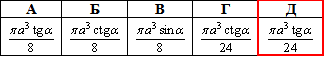
Розв'язання: Об'єм конуса обчислюють за формулою:
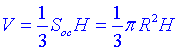, де 
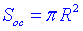– площа основи конуса (площа круга);
H=SO – висота конуса. З
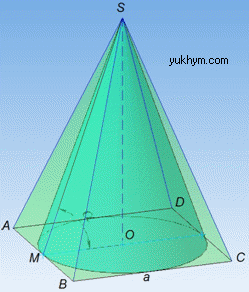
Конус вписаний у піраміду, якщо основа конуса вписана в основу піраміди, а висота конуса дорівнює висоті піраміди.
Маємо правильну чотирикутну піраміду SABCD з кутом alpha нахилу бічної грані до площини основи.
В основі піраміди лежить правильний чотирикутник (тобто квадрат) ABCD з довжиною сторони a.
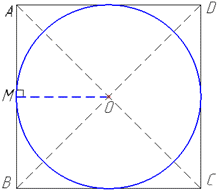
Проведемо відрізок MO⊥AD. Оскільки висота SO піраміди перпендикулярна до площини основи (квадрата ABCD), то вона перпендикулярна до кожної прямої, що належить площині основи, тому SO⊥MO.
Проведемо відрізок (похилу) SM. Оскільки MO⊥AB, то за теоремою «про три перпендикуляри» SM⊥AB, звідси SM – висота бічної грані правильної чотирикутної піраміди – апофема піраміди;
∠SMO=alpha – кут нахилу бічної грані до площини основи.
У квадраті MO⊥AB, де точка O – центр квадрата (точка перетину діагоналей), тому (за властивістю квадрата) MO||AD і MO=AD/2=a/2 (це доводиться на основі того, що MO – середня лінія трикутника ABD).
Оскільки MO⊥AB, то R=MO=a/2 – радіус вписаного круга в основу піраміди, тобто радіус основи конуса.
Розглянемо прямокутний трикутник MOS (∠MOS=90), в якому MO=a/2 – катет прилеглий до кута ∠SMO=alpha.
За означенням тангенса гострого кута прямокутного трикутника знайдемо протилежний катет SO – висоту піраміди:
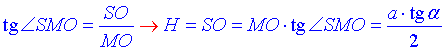
Обчислимо об'єм заданого конуса:
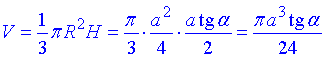
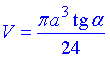– об'єм конуса, вписаного в правильну чотирикутну піраміду.
Це завдання складніше, адже потрібно виводити формулу об'єму через тригонометричні формули.
Але якщо Ви правильно виконали рисунок до задачі, то наведені формули вивести не так і важко.
Відповідь: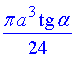 
– Д.
Задача 39.20 Трикутник зі сторонами 3 см, 4 см і 5 см обертається навколо найбільшої сторони.
Знайти площу поверхні обертання.
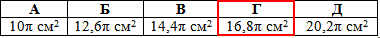
Розв'язання: Маємо прямокутний ΔABC (∠ABC=90), в якому AB=4 см і BC=3 см катети і AC=5 см – гіпотенуза, оскільки
AC2=AB2+BC2, 52=42+32. Допоміжний рисунок, який дасть змогу уявити та візуалізувати поверхню обертання наведено далі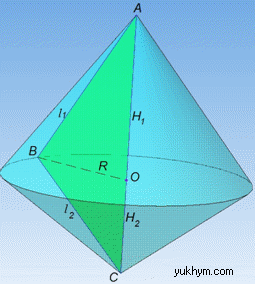
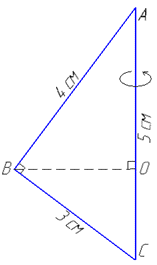
Тіло, яке утвориться при обертанні прямокутного ΔABC навколо гіпотенузи AC складається з двох конусів зі спільною основою з центром O.
Далі виписуємо прості закономірності, які легко отримати за побудовою до завдання.
Проведемо відрізок BO⊥AC, тоді R=BO – висота ΔABC є радіусом основ конусів.
Висоти конусів H1=AO і H2=BO – відрізки, на які розбиває центр основи гіпотенузу AC.
Твірна більшого конуса l1=AB є відповідно більшим катетом ΔABC, а твірна меншого конуса l2=BC є відповідно меншим катетом ΔABC.
Оскільки ΔABC – прямокутний, то
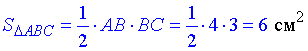– площа;
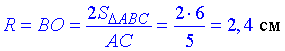– висота ΔABC і радіус основи конусів.
Площа бічної поверхні конуса обчислюється за формулою:
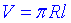, де R – радіус основи і l – твірна конуса.
Площа поверхні обертання (яка складається з двох конусів) рівна:
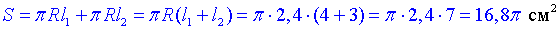
Якщо потрібно, то можна "Pi" записати числом, та у відповідь записати наближене значення площі десятковим числом.
Відповідь: 16,8π см2 – Г.
Задача 39.27 Твірна конуса утворює з його основою кут 30, а площа перерізу, що проходить через твірні, кут між якими 120, дорівнює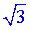 
.
Знайти об'єм V конуса. У відповідь записати V/π.
Розв'язання: Добре запам'ятайте формулу об'єму конуса – це третина добутку площі основи (круга) на висоту:
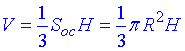
Рисунок до задачі та позначення мають наступний вигляд
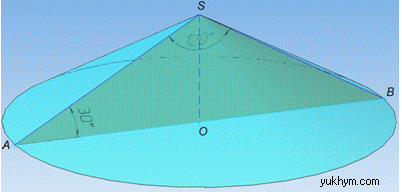
З вхідних даних маємо радіус основи конуса R=AO=BO і твірними SA=SB.
Кут нахилу твірної до площини основи – це кут між твірною і радіусом основи (оскільки радіус основи конуса є проекцією твірної на площину основи), тобто ∠SAB=30.
Розглянемо осьовий переріз ΔSAB (дивись І абзац задачі 39.1), звідси знайдемо кут між твірними SA і SB (за теоремою про суму кутів трикутника і рівності кутів при основі AB рівнобедреного ΔSAB):
∠ASB=180-2•∠SAB=180-60=120.
Отже, переріз, що проходить через твірні, кут між якими 120 є осьовим з площею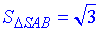 
(за умовою задачі).
Розпишемо площу осьового перерізу через синус кута при вершині:
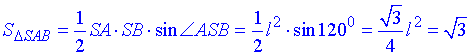
Звідси l2/4=1, L2=4, отже l=SA=2 – твірна конуса.
Розглянемо прямокутний трикутник AOS (∠AOS=90), в якому SA=2 – гіпотенуза, ∠SAO=30 – кут прилеглий до катета AO=R і протилежний до катета SO=H.
За означенням косинуса і синуса гострого кута прямокутного трикутника знайдемо прилеглий AO=R – радіус основи і протилежний катет SO=H – висоту конуса:
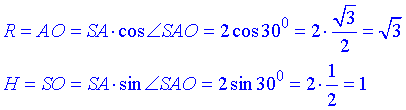
Отже,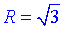 
– радіус основи і H=1 – висота заданого конуса.
Можемо знайти об'єм конуса:
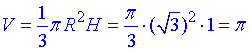
У відповідь записуємо нормоване на "Pi" значення:
V/π=1.
Відповідь: 1.
Задача 39.30 Знайти об'єм V тіла, яке утворюється при обертанні ромба зі стороною 1 і гострим кутом 60 навколо меншої діагоналі.
У відповідь записати V/π.
Розв'язання: Маємо ромб ABCD, в якому AB=BC=CD=AD=1 – сторона і ∠ADC=∠ABC=60 – гострий кут між сусідніми сторонами;
AC=1 – менша діагональ (оскільки ΔADC з кутом 60 є рівностороннім за властивістю ромба),
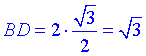– більша діагональ (обчислили як висоту рівностороннього ΔADC зі стороною 1 і помножили на 2 за властивістю діагоналей ромба).
Тіло обертання матиме наступний вигляд
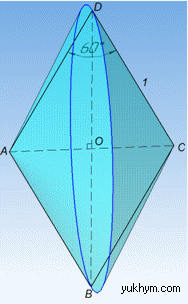
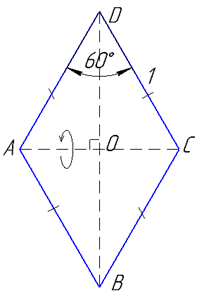
За властивістю діагоналей ромба маємо:
півдіагоналі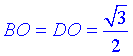 
і AO=CO=1/2.
Тіло, яке утвориться при обертанні ромба ABCD навколо меншої діагоналі AC складається з двох конусів зі спільною основою з центром O, де R=BO=DO є радіусом основи конусів;
H=AO і H=BO є висотами конусів, оскільки діагоналі ромба перпендикулярні (за властивістю).
Звідси слідує, що ці два конуси рівні, а тому їх об'єми також рівні.
Отримали:
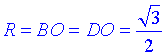– радіус основи
та H=AO=CO=1/2 – висоту конуса.
Об'єм конуса знаходимо за відомою формулою:
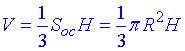
де R – радіус основи і H – висота конуса.
Підставляємо та обчислюємо об'єм утвореного тіла обертання:
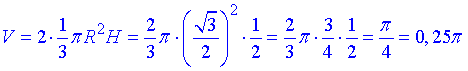
V/π=0,25.
Відповідь: 0,25.
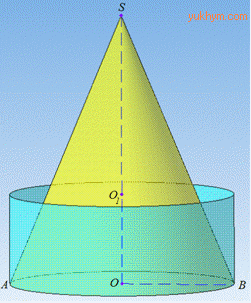
Завдання 23. ЗНО 2018 Циліндр і конус мають рівні об'єми та рівні радіуси основ. Площа основи циліндра дорівнює 25π см2, а його об'єм - 100π см3. До кожного початку речення (1–4) доберіть його закінчення (А–Д) так, щоб утворилося правильне твердження.
Розв'язування:Побудуємо конус та цилідр зі спільною основою.
1. Об'єм циліндра знаходимо за формулою:
V=Soc•Hc, звідси
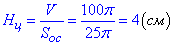
Висота циліндра дорівнює 4 см. А
2. Об'єм конуса:
V=Soc•Hk/3, звідси
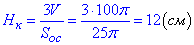
Висота конуса дорівнює 12 см. Г
3. Площа основи циліндра:
Soc=πR2, звідси
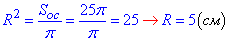
Радіус основи циліндра дорівнює 5 см. Б
4. У прямокутному ΔSOB (∠SOB=90) за теоремою Піфагора знайдемо BS,(твірну):
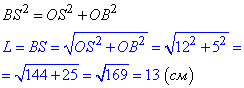
Твірна конуса дорівнює 13 см. Д
Як Ви могли переконатися – завдання не є важкими, потрібно лише правильно виконати побудову конусів до завдань, а решта все слідує з геометрії.
Далі проаналізуємо задачі на повну площу конуса та площу бічної поверхні.
