Квадрат і коло – дві найпростіші фігури геометрії, властивості яких повинні знати усі. Квадрат є частковим випадком чотирикутників, прямокутників, паралелограмів, ромбів, а вирізняється рівними сторонами і прямими кутами.
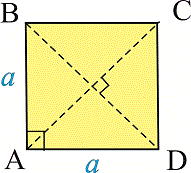
Квадрат найбільш симетрична фігура серед всіх чотирикутників.
Властивості квадрату
Властивості квадрата - це основні признаки, які дозволяють розпізнати його серед прямокутників, ромбів, чотирикутників
- У квадрата всі сторони і кути рівні AB=BC=CD=AD.
- Протилежні сторони паралельні між собою
- Кути між сусіднвми сторонами прямі.
- Діалоналі квадрата рівні і перетинаються під прямим кутом.
- Діагоналі є одночасно бісектрисами кутів квадрата.
- Точка в якій перетинаються діагоналі є центром квадрату, крім цього – центром вписаного та описаного кіл.
- Діагоналі ділять квадрат на чотири однакові рівнобедрені прямокутні трикутники.
Площа квадрата
Найбільше прикладів в шкільному курсі при вивченні квадрату пов'язано з обчисленням його площі та периметру. Вам може здатися, що для обчислення площі достатньо знати одну формулу S=a*a і цього вистачить для всіх задач, проте це не так. Оскільки найшвидше інформація сприймається і вивчається візуально, то ми об'єднали всі величини квадрата, які Вам прийдеться обчислювати і намалювали прості і зрозумілі рисунки з формулами.
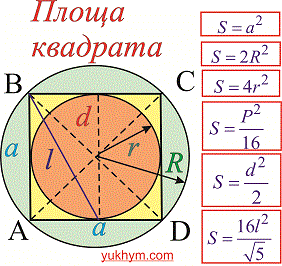
Більшість позначень Вам зрозуміла, але повторимо їх знову
a– сторона квадрата;
d– діагональ;
P– периметр;
S– площа;
R– радіус описаного кола;
r– радіус вписаного кола;
l– відрізок зображений на рисунку( часто використовується в складних прикладах).
Формули площі квадрата, які наведені нижче дають можливість її обчислення через периметр, сторону, діагоналі, радіуси.
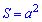
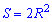
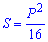
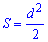
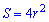
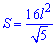
Вони не надто складні і кожна з них може стати Вам в нагоді для обчислення площі квадрата.
Периметр квадрата
Що може бути простіше за обчислення периметру квадрата, якщо відомо його сторону. Однак, якщо задано лише діагональ, площу, радіус то знаходження периметру не таке очевидне. Наведений нижче рисунок містить найбільш необхідні формули для обчислення периметру квадрата
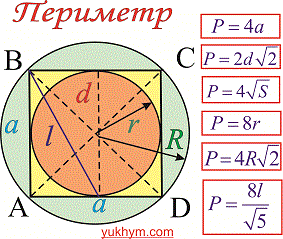
Формули периметру через діагональ, площу, радіуси і т.д. наведені нижче
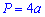
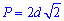
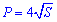
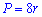
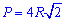
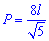
Діагональ квадрата
Діагональ квадрата може мути виражена через радіуси вписаного, описаного кіл, сторону, периметр , площу наступними формулами.
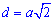
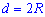
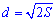

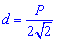
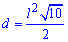
В ролі довідника формул для обчислення діагоналі квадрата можете використовувати наступний рисунок.
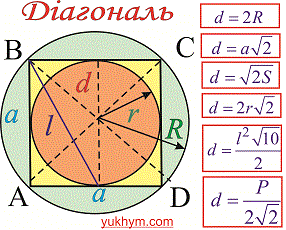
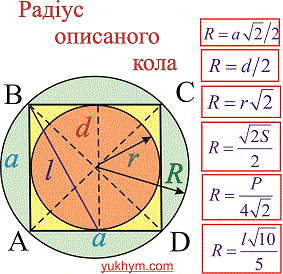
Радіус описаного кола
Найпростіша формула радіуса описаного кола R=d/2, тобто радіус рівний половині діагоналі квадрата. Всі наступні формули, які допоможуть визначити радіус описанного кола містять корені, однак при обчисленнях незамінні.
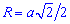
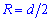
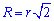
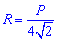
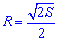
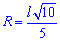
Нижче зображено рисунок-схема з наведеними усіма формулами.
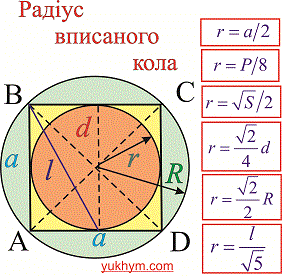
Радіус вписаного кола у квадрат
Радіус вписаного кола з рисунку рівний половині його сторони.
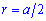
Також він рівній одній восьмій частині периметру. Залежності для знаходження радіусу вписаного кола через площу, діагональ, радіус описаного кола містять ірраціональності. Однак і в умовах прикладів величини, що відомі для обчислення радіусу, як правило, задані з коренями або такими, які легко спрощуються( наприклад 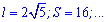 ).
).
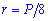
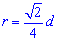
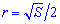
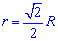
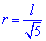
Чорновик-підказка формул радіуса вписаного в квадрат кола наведена нижче
Якщо ж задано діаметр вписаного або описаного кола, то ділимо на два і можемо застосовувати в наведених формулах. Це Ви думаю пам'ятаєте.
Бонус для всіх школярів та студентів. Усі кольорові графіки з формулами площі квадрата, його периметру, діагоналі, вписаного та описаного радіусів Ви можете завантажити за посиланням унизу.
Роздруковуйте формули та користуйтеся в навчанні.
Сподобався матеріал – поділися посиланням з друзями.


