Без похідної неможливо визначити проміжки зростання та спадання функції, точки перегину, якщо такі існують. Суть таких досліджень – полегшити побудову графіка функції, адже якщо Ви знайшли вказані проміжки то на їх межі функція має локальні екстремуми і залишається знайти в них значення і побудувати графік функції. Правила на знаходження інтервалів зростання функції достатньо прості та зрозумілі кожному.
Ознака зростання функції
Якщо похідна функції більша нуля f'(x)> 0 на деякому проміжку, то функція f (x) зростає на цьому проміжку.
І обернене твердження.
Ознака спадання функції
Якщо похідна функції від'ємна f'(x) < 0 на деякому інтервалі, то функція f (x) спадає на даному інтервалі.
Застосування похідної на прикладах
Приклад 1. Знайти проміжки зростання та спадання функції
f(x)=x3-6*x2-15x.
Розв'язання: Обчислюємо похідну функції за змінною
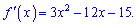
Прирівняємо похідну до нуля та визначимо стаціонарні точки
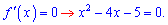
За теоремою Вієта корені квадратного рівняння рівні x=-1; x=5.
Точки розбивають числову вісь на три інтервали
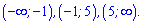
Знак похідної визначаємо підстановкою точки з інтервалу.
Запам'ятайте: для швидкого визначення знаку похідної завжди вибирайте нуль, якщо він не є стаціонарною точкою або іншу точку, в якій легко обчислити значення похідної.
В нулі похідна менша нуля
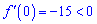
отже на інтервалі (-1;5) функція спадає, а на двох сусідніх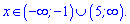 
зростає
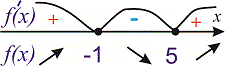
Графік функції має вигляд
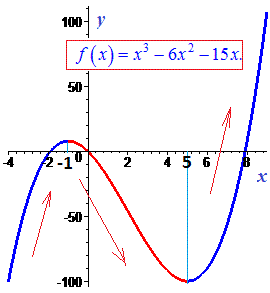
Приклад 2. Дослідити функцію f(x)=x4-8*x2-5 та знайти проміжки зростання.
Розв'язання: Задана функція є парною
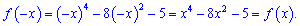
Знайдемо інтервали монотонності функції. Для цього обчислимо похідну
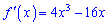
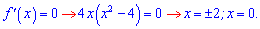
Отримали три точки, які розбивають числову вісь на 4 інтервали
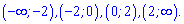
Знак похідної визначаємо підстановкою одиниці
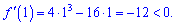
Отже на інтервалі (0;2) функція спадає, на сусідніх інтервалах знаки похідної чергуються
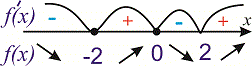
У відповіді отримаємо 2 інтервали зростання функції
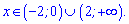
Для наочності графік функції наведено нижче
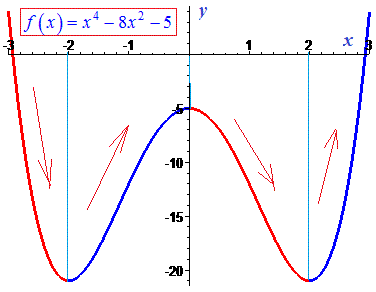
Інше застосування похідної відноситься до знаходження інтервалів опуклості та вгнутості графіка функції. При цьому потрібно знаходити другу похідну та виконувати відповідний аналіз.
