Дослідження функцій повинно починатися з встановлення області визначення та інтервалів монотонності. Для цього студент повинен володіти добрими знаннями поведінки елементарних функцій та наступним теоретичним матеріалом.
Функція y=f(x) називається зростаючою на інтервалі (a; b), якщо для будь-яких двох точок x1 і x2 з цього проміжку, і таких, що x1<x2, виконується нерівність
f(x1)<f(x2).
Для того щоб функція y=f(x) була спадною на інтервалі (a; b) необхідно, щоб для будь-яких x1 і x2, що належать до цього інтервалу, і відповідають умові x1<x2, справджувалася нерівність
f(x1)>f(x2) .
Як зростаючі, так і спадні функції називаються монотонними, а інтервали, в яких функція зростає або спадає – інтервалами монотонності.
Область зростання і спадання функції y=f(x) характеризується знаком її похідної: якщо у деякому інтервалі f'(x)>0, то функція зростає в цьому інтервалі;
якщо ж f'(x)<0 – то функція спадає в цьому інтервалі.
Інтервали монотонності можуть прилягати один до одного або точками, де похідна дорівнює нулю або точками, де похідна не існує. Ці точки називаються критичними точками.
Для того, щоб знайти інтервали монотонності функції f(x) потрібно:
1) знайти область визначення функції D(f) ;
2) обчислити похідну даної функції;
3) знайти критичні точки з рівняння f'(x)=0 та за умови, що f'(x) не існує;
4) розділити критичними точками область визначення на інтервали і у кожному з них визначити знак похідної.
На інтервалах де похідна додатна, функція зростає, а де від'ємна – спадає.
Приклади. Розглянемо завдання із збірника В.Ю. Клепко, В.Л. Голець "Вища математика в прикладах і задачах" на знаходження області визначення функції.
1. (3.36.10) 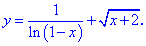
Розв'язування: Функція існує в усіх точках де визначений логарифм і він не перетворюється в нуль, а також де підкоренева функція приймає невід'ємні значення. На основі цього знаходимо
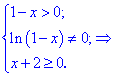
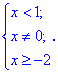
Отже, областю визначення будуть 2 інтервали
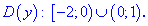
Щоб бачити, що собою уявляють графіки функцій побудуємо їх в математичному пакеті Мейпл17. Для цього наведемо необхідний на початку код, щоб обнулити попередні дані:
> restart;with(plots):
> q1:=plot(1/ln(1-x)+sqrt(x+2),x=-3..2,color=red):
> display(q1);
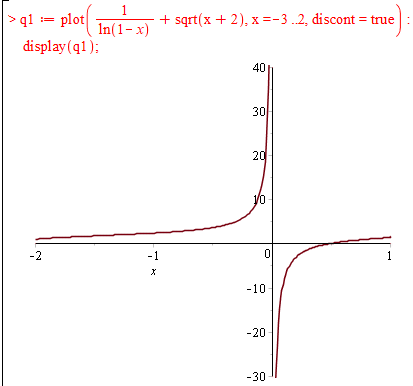
2. (3.36.11) 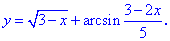
Розв'язування: З підкореневою функцією поводимося як і в попередньому прикладі, а функція arcsin(x) визначена на проміжку [-1; 1]. Встановлюємо область визначення
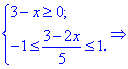
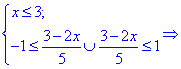
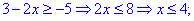
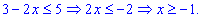
Єдиним проміжком, який задовільняє ці умови є [-1;3]
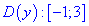
Так як функція не має асимптот, то її графік в Мейплі побудуємо за наступним кодом
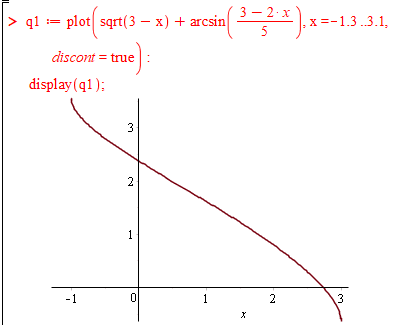
3. (3.36.13) 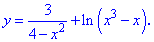
Розв'язування: Область визначення функції знаходимо з умов обмеження на знаменни дробової фунції та логарифм
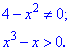
Перша умова дає дві точки
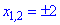
в яких функція не існує.
З другої умови отримаємо 3 точки
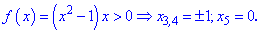
Дослідимо поведінку функції в інтервалах, на які розбивають задані точки. Для цього вибираємо довільні точки x0 з інтервалів та перевіряємо знак f(x0)
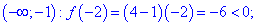
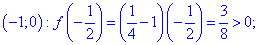
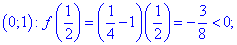
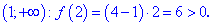
Функція f(x) приймає додатні значення в інтервалах
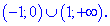
Разом з першою умовою, матимемо наступну область визначення
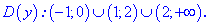
Наведемо код в пакеті Мейпл для побудови графка функції.
Для побудови вертикальних асимптот використовуйте команду impliciplot() з наведеними на рисунку параметрами.
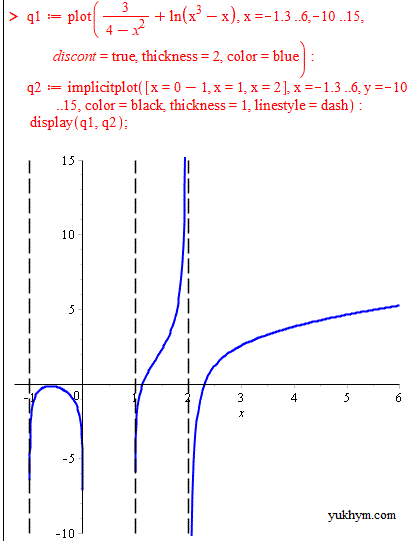
Візуалізація даних, графків функцій і т.д. відіграє важливу роль в засвоєнні правил, навчального матеріалу, тому навчіться користуватися одним з поширених патематичних пакетів MatLab, MathCad, Maple.
Розглянемо приклади зі збірника задач Дубовика В.П., Юрика І.І. "Вища математика" на дослідження монотонності функції.
І. (5.705) Показати, що функція 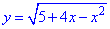 зростає на інтервалі (-1; 2) таі спадає на інтервалі (2; 5) .
зростає на інтервалі (-1; 2) таі спадає на інтервалі (2; 5) .
Розв'язування:1) Областю визначення функції буде множина значень для яких підкоренева функція приймає невід'ємні значення.
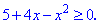
Розв'яжемо квадратне рівняння через дискримінант
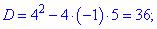
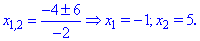
Визначимо знак підкореневої функції на всьому інтервалі R
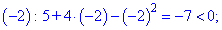
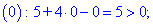
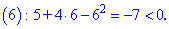
Таким чином отримаємо наступну область визначення
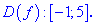
2) Знайдемо похідну
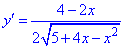 .
.
3) Прирівняємо її до нуля та знайдемо критичні точки:
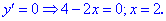
Не варто забувати і про точки в яких похідна не існує. Такими корені рівняння в знаменнику
x1=-1; x2=5.
Отже похідна існує на інтервалі (1; 5) і в точці x=2 змінює знак.
4) Знаки похідної: підставляємо x=0 в похідну y'
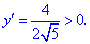
Отже на інтервалі (-1; 2) функція зростає, а на (2; 5) - спадає.
Пакет with(plots) в Мейплі дозволяє об'єднувати як завгодно багато графіків за допомогою функції display(). Тому на інтервалі де функція зростає побудуємо криву червоним кольором, а де спадає - синім кольором.
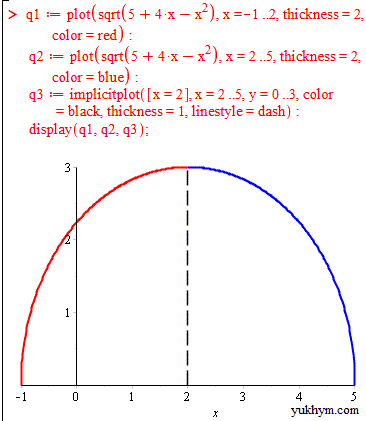
Нам для цього довелося скопіювати один рядок коду, та змінити параметри color на red та blue відповідно.
ІІ. (5.715) Знайти інтервали монотонності функції
y=x-ln(x+2).
1. Областю визначення буде множина точок  для яких існує логарифм функція. На основі цього матимемо
для яких існує логарифм функція. На основі цього матимемо
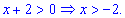
Отже 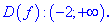
2) Обчислюємо похідну функції
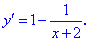
3) Знаходимо критичні точки
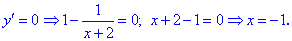
Інша точка, де похідна не існує це x=-2, вона не належить області визначення функції.
Таким чином отримали два інтервали монотонності 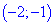 та
та 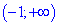 .
.
4) Вияснимо де функція зростає, а де спадає. Підставимо точки x=0 та x=-1,5 у вираз для похідної
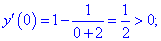
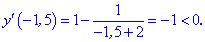
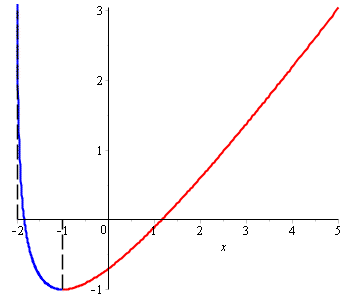
Досліджувана функція на інтервалі (-2; -1) спадає і від -1 до безмежності 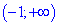 зростає.
зростає.
Приведемо рисунок графіка функції, виконаний в математичному пакеті Мейпл.
І запам'ятайте, що де б Ви не йшли на роботу, завдання будуть складнішими, а оформлення результатів у вигляді звітів та презентацй вимагатимуть робити якісними. Тому паралельно з навчанням вивчайте графічні редактори, математичні пакети та одну з мов програмування.
При дослідженні функцій на монотонність визначте всі критичні точки в яких похідна рівна нулю або не існує. Також не забувайте при цьому враховувати область визначення функції. Решта залежить від Ваших знань властивостей елементарних функції, оскільки саме на їх основі побудовані всі завдання, які Вам задають викладачі.


