Для практичного ознайомлення з таблицею основних формул диференціювання розглянемо популярні варіанти завдань на похідні.

Приклад 1. Обчислити похідні функцій
1) ![]()
Розв'язок. За формулами диференціювання (1), (3), (8) знаходимо похідну полінома
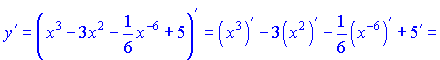
![]()
Похідна від сталої рівна нулю. Це правило найлегше, тому запам'ятайте його в числі перших.
2) 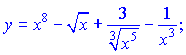
Розв'язок. Вводимо дробові та від'ємні степені, та перетворюємо задану функцію до вигляду
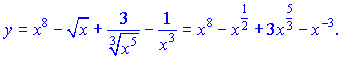
Використовуючи формули (3), (4), (7), знаходимо похідні
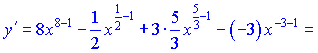
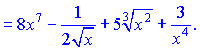
Вкінці записуємо результат через корені в знайдених степенях.
3) 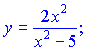
Розв'язок. Похідну дробової функції знаходимо за правилом похідної частки (6):
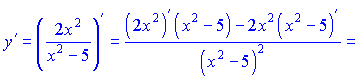
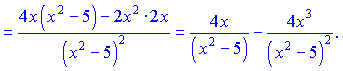
Обчислення не складні – в результаті диференціювання отримаємо різницю простих дробів 1 та 2 типу.
4) ![]()
Розв'язок. Похідну кореневої залежності ![]() шукаємо за правилом для складної функції
шукаємо за правилом для складної функції
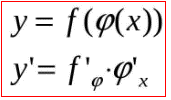
Тому вираз під коренем приймаємо за нову змінну φ=3+x5, беремо похідну від кореня по φта множимо на похідну від φ=3+x5 по "іксу":
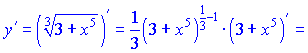
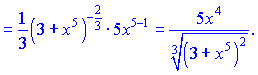
При роботі з дробовими показниками будьте уважні!
5) ![]()
Розв'язок. Похідну від добутку кореня на поліном знаходимо за правилом добутку функцій (5) та формулою похідної від складної функції. В результаті отримаємо наступні перетворення
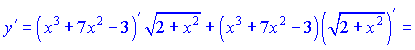
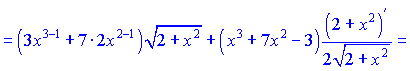
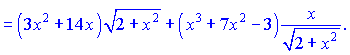
Записів багатенько, проте на практиці буде не легше, тож вивчайте правили диференціювання.
6) y=2sin(2x^3)
Розв'язок. За формулою похідної від складної функції отримаємо
![]()
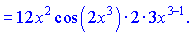
Останній вираз можете спростити, підсумувавши показники змінної.
7)y=(3x3-5x2+6)2
Розв'язок. Багато студентів, які ще добре не знають правил, спочатку підносять до квадрату вираз в дужках, а потім проводять диференціювання. Це неправильно, довго і важко. Скориставшись правилом диференціювання складної функції, отримаємо похідну від квадрата помножену на похідну кубічної функції
![]()
![]()
![]()
Якщо Ви будете підносити до квадрату, а потім диференціювати то отримаєте многочлен, який ще треба буде зводити до компактного вигляду. Результат буде правильний, але навіщо йти складним шляхом, якщо за нас вже давно придумали правила диференціювання, які спрощують обчислення. Вивчайте їх та користуйтеся на практиці.
Приклад 2 Знайти похідну першого порядку
y=5x^3-x^2+6x-4.
Розв'язування: За правилом похідної суми маємо
y'=(5x3-x2+6x-4)'=(5x3)'-(x2)'+(6x)'-(4)'=
=5·3x2-2x+6=15x2-2x+6.
Хто не розуміє чому так, рекомендуємо переглянути формули (1-8) крім (5-7), якщо далі не знаєте чому так вийшло - перегляньте попередні уроки.
Приклад 3 Знайти похідну функції
y=tg(7x+x^2).
Розв'язування: Під косинусом маємо не сам аргумент "x" як у формулі (16), а вираз 3x+1.
Щоб знайти похідну перепозначимо:
u=7x+x2, y=tg(u).
Тоді за правилом похідної складеної функції
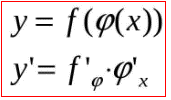
диференціюємо задану функцію
y'=(tg(u))'·u'x =1/cos2(u)·(7x+x2)'=
=(2x+7)/cos2(7x+x2).
Приклад 4 Знайти похідну
y=cos(3x+1).
Розв'язування: Алгортм обчислення похідної ідентичний до попереднього прикладу, тому на ньому зупинятися не будемо.
Краще уважно розберіть формулу
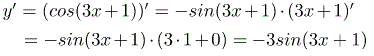
Думаю, що під силу знайти усім.
А щоб краще засвоїти матеріал, потрібно кілька завдань обчислити самостійно:
y=у3x-1;
y=√(2x+5);
y=sin(x2-2x-8);
y=ln(2x+7)·(3x2-5x+6);
y=√x/(x5+4x3+2).
В наступних уроках проаналізуємо ще більше готових похідних та пояснень як їх знайти в мат. пакетах та на онлайн сервісах.


