Для охвата всего материала мы собрали много примеров из студенческой практики, модулей, контрольных, заказов и попытаемся здесь разъяснить, как и в каких случаях применять приведенные алгоритмы.
Пример 1. Вычислить предел последовательности:
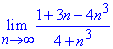
Решение: При подстановке бесконечности получим неопределенность вида бесконечность разделить на бесконечность (∞/∞). Разделим числитель и знаменатель на переменную в наибольшей степени и сократим на нее. В результате избавимся от неопределенности, а слагаемые что останутся, будут стремиться к нулю при больших номерах последовательности
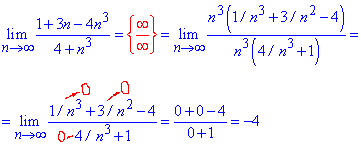
Все числа, что останутся и укажут куда стремится предел.
Пример 2. Вычислить предел последовательности:
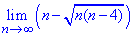
Решение: При прямой подстановке бесконечно большого номера получим неопределенность бесконечность минус бесконечность (∞-∞).
Правило раскрытия такого типа неопределенности хорошо расписано в литературе и заключается в умножении и разделении неопределенности на множитель, сопряженный к ней.
Как правило, такие примеры содержат корни и чтобы их лишиться используем умножение на сопряженный множитель, что приводит к разности квадратов или кубов, в то время в знаменателе (или числителе) получим выражение с корнем, которое не содержит неопределенности.
Далее из числителя и знаменателя выделяем доминирующий множитель и упрощаем на него.
Все числа, что останутся и составят предел последовательности.
На языке формул этому отвечает запись
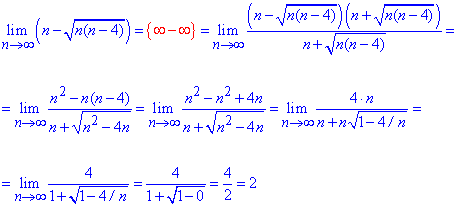
Пример 3. Найти предел функции:
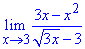
Решение: При подстановке x=3 получим неопределенность 0/0.
Это означает, что и числитель и знаменатель содержат особенность.
Для раскрытия неопределенности выделим в числителе (x-3), а знаменатель умножим и разделим на сопряженное выражение 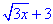 .
.
В результате получим множитель (x-3), на который упрощаем дробь. Далее предел вычисляется методом подстановки переменной
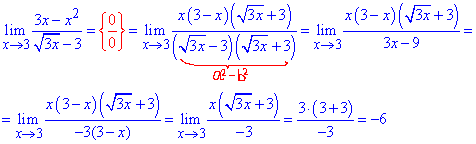
Пример 4. Найти предел функции:
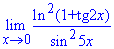
Решение: Задание для большинства студентов чрезвычайно сложное, а все потому что необходимо свести неопределенность типа 0/0 до известных случаев.
В результате преобразования функций получим выражения вида ln(1+x)/x, tan(x)/x, sin(x)/x при переменной стремящейся к нулю.
Далее выделяем первую замечательный предел и ее следствие, затем расписываем через произведение известных пределов.
Все остальное сводится к произведению единиц и отдельного множителя, который и является пределом заданной функции.
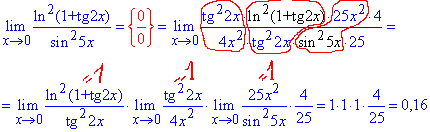
Внимательно разберите приведенный пример, он Вас многому научит.
На практике довольно трудно найти условие, которое бы объединяла несколько формул, поэтому учитесь на сложных примерах.
Тогда точно не будет сложностей в исчислении простых примеров.
Пример 5. Вычислить предел функции:
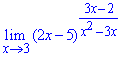
Решение: Подстановка 3 в функцию дает особенность вида единица в степени бесконечность (1^∞). Для ее раскрытия и в функции в скобках, и в дроби, что является показателем выделяем часть, что вносит особенность (х-3).
Далее, для упрощения манипуляций с выражениями делаем замену переменных x-3=t, новая переменная при этом стремится к нулю.
После этого выделяем второй замечательный предел и ищем лимит показателя, что остался.
На этом разбор распространенных примеров, которые распространены в учебной практике не завершается.
В соседней публикации будут проанализированы новые алгоритмы вычислений, и примеры пределов функций та последовательностей, которые помогут Вам быстрее освоить теоретический материал и подготовиться к контрольной, модулю, экзамене.
Пример 6. Вычислить предел последовательности:
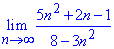
Решение: При подстановке бесконечности получим неопределенность вида бесконечность поделить на бесконечность (∞/∞).
Раскрыть особенность возможно двумя способами: по правилу Лопиталя или выделением множителей, которые вносят наибольший вклад в числителе и знаменателе дроби.
По правилу Лопиталя получим
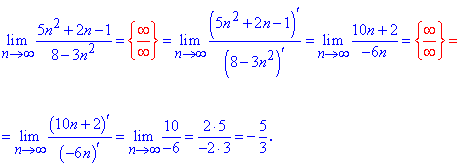
По второй методике предел последовательности равен
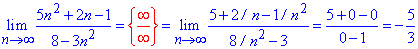
Значения совпадают, как первая схема так и вторая не тяжелые для применения.
Однако часто в одних задачах требуют вычислить предел последовательности по правилу Лопиталя.
В других наоборот – не используя правило Лопиталя найти предел.
Пример 7. Вычислить предел последовательности:
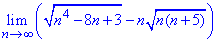
Решение: Имеем разницу двух корней, которые при подстановке переменной дают особенность вида бесконечность минус бесконечность (∞-∞).
Для устранения особенности умножим и разделим корневую зависимость на сопряженное выражение (сумму корней). В результате придем к разности квадратов в числителе.
Повторная подстановка дает особенность вида бесконечность разделить на бесконечность.
Чтобы избавиться от особенности выделяем доминантные множители в числителе и знаменателе и оцениваем, что в итоге перевешивает (доминирует).
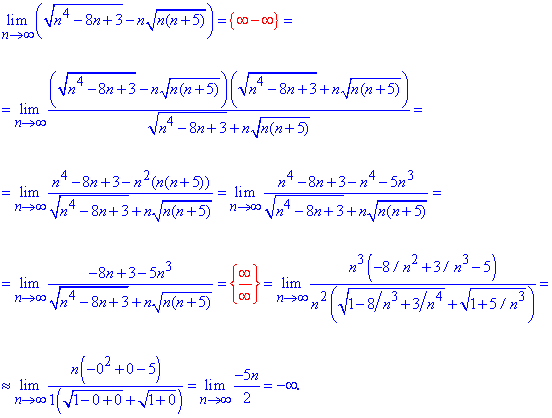
Получили, что в числителе старший степень чем в знаменателе, поэтому предел стремится к бесконечности. Но важно еще выяснить к плюс бесконечности или к минус бесконечности. Для этого следует проанализировать вклад слагаемых в скобках.
Пример 8. Найти предел функции:
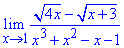
Решение: При подстановке единицы получаем особенность вида ноль разделить на ноль {0/0}.
Для ее раскрытия разницу корней в числителе умножим на сумму корней, чтобы избавиться от иррациональности. На ту же сумму корней следует умножить знаменатель, чтобы манипуляциями не изменить значение предела.
Далее анализируем знаменатель – он содержит полином, который в свою очередь имеет в разложении множитель (x-1) (как особенность).
Разложим полином на простые множители и заменим ими соответствующую часть дроби.
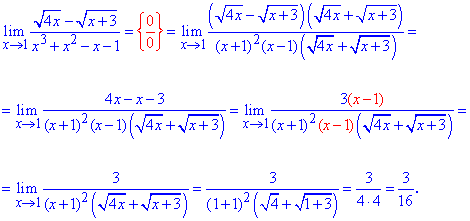
Далее упрощаем числитель и знаменатель на общий множитель (x-1), и методом подстановки находим предел функции, что осталась.
Пример 9. Найти предел функции:
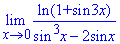
Решение: В заданиях, где переменная стремится к нулю и имеем дробь, содержащий логарифмы или тригонометрические функции следует искать возможность получить первую замечательный предел, следствия второго и первого лимита или сочетание обоих вариантов. Этот пример сочетает все возможное, что может Вас ждать на практике.
Простая подстановка показывает, что имеем лимит с неопределенностью вида {0/0}. Для устранения неопределенности и возведения сперва логарифма к виду ln(1+y)/y, делим и умножаем на sin(3x). Чтобы этот же синус в числителе свести под некую формулу, разделим и умножим на (3x). Таким образом получим часть, которая отвечает за формулу первого замечательного предела.
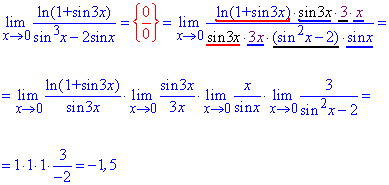
Разницу синусов, что была в начале в знаменателе дроби распишем, выделив sin(x) как общий множитель.
Далее переходим к произведению пределов, сгруппировав предварительно соответствующие дроби под формулы замечательных пределов.
Все остальные ответы, которые Вас интересуют дает приведенная формула расчетов.
Пример 10. Найти предел функции:
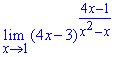
Решение: Прямая подстановка единицы показывает, что имеем неопределенность вида единица в степени бесконечность 1^∞. А это означает, что имеем дело со вторым замечательным пределом.
Для устранения особенности в скобках и показателе выделим выражения, содержащие (x-1). После этого делаем замену переменных, t=x-1, при этом новая переменная стремится к нулю. Далее в показателе выделяем множитель, который является обратно пропорциональным к слагаемому в дужках (1/4t), это даст нам экспоненту.
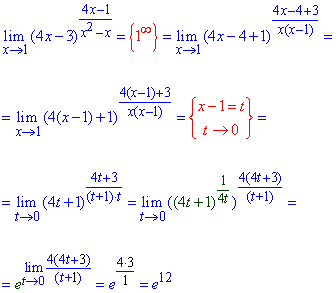
Все, что останется множителем в показателе даст степень экспоненты в предельном переходе (12).
Хорошо проанализируйте приведенный пример, он на самом деле не такой тяжелый, если внимательно разобраться.
В новых публикациях Вы получите ответы на другие вопросы, которые могли у Вас возникнуть в связи с тем, что рассмотрено всего 5 примеров.
Пример 21 Вычислить предел последовательности:
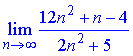
Решение: Для вычисления предела частки полиномов выносим n^2 из числителя и знаменателя дроби и упрощаем на них.
В итоге останутся числа и бесконечно малые величины. Лимит последовательности равный доле постоянных (=6).
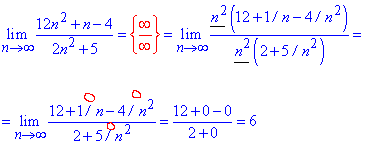
Попробуйте самостоятельно этот же пример вычислить по правилу Лопиталя.
Пример 22 Определить лимит последовательности
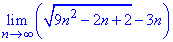
Решение: Предел последовательности вычисляем методом умножения на сопряженное выражение. Таким образом получим разность квадратов и избавимся от корней в числителе.
Далее из числителя и знаменателя дроби выносим n и упрощаем на него. После этого оцениваем дробь при предельном переходе.
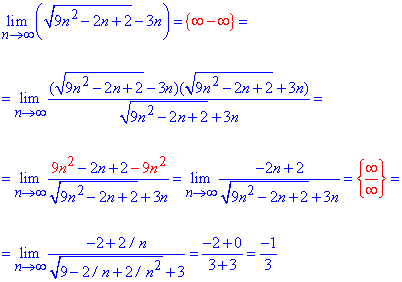
Пример 23 Найти предел функции
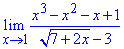
Решение: Лимит функции в точке дает неопределенность вида {0/0}. В числителе полином раскладываем на простые множители, в знаменателе избавляемся от иррациональности умножением на сопряженное выражение. Таким образом избавляемся особенности в знаменателе, однако она остается в числителе. В результате предел функции в точке равен нулю.
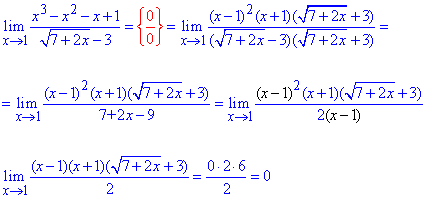
Пример 24 Свести под важные пределы и вычислить
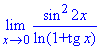
Решение: Предел функции синус логарифма дает особенность {0/0}. Для ее раскрытия следует заданную функцию свести под первый и второй замечательные пределы и их следствия.
Для этого умножуєм и делим на выражения, которых не хватает для применения замечательных пределов. Далее группируем и сводим к произведению пределов, часть из которых равна 1.
Все что останется и составляет предел функции.
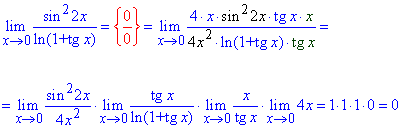
Пример 25 Чему равен лимит функции?
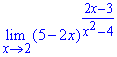
Решение: Функция имеет особенность – единицу в степени бесконечность. Раскрываем ее методом выделения второго замечательного предела, который равен экспоненте.
Для этого выделяем повсюду выражения (x-2), что вносят особенность, а дальше переходим к новой переменной t=x-2.
В показателе выделяем обратный множитель (-1/2t) до слагаемого при единице в скобках (1-2t).
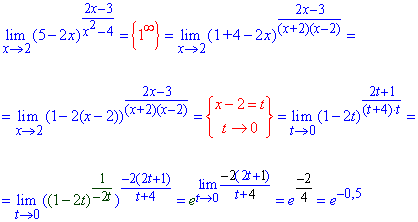
Таким образом, получим экспоненту в степени - лимит функции, что осталась.
Пример 26 Вычислить предел последовательности
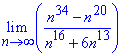
Решение: Если переменная стремится к бесконечности  , то наибольший вклад вносит переменная в старшем степени. Выделим их в числителе и знаменателе
, то наибольший вклад вносит переменная в старшем степени. Выделим их в числителе и знаменателе
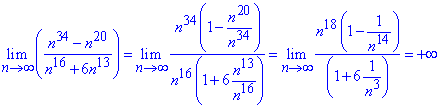
Далее, если в числителе старший степень, то предел стремится к бесконечности.
Пример 27 Найти границу
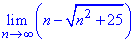
Решение: Если подставить бесконечность в последовательность получим неопределенность 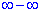 . Чтобы ее раскрыть, разделим и умножим на выражение, чтобы в числителе получить разность квадратов
. Чтобы ее раскрыть, разделим и умножим на выражение, чтобы в числителе получить разность квадратов
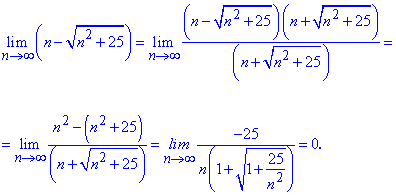
Граница равна нулю, так как степень знаменателя выше степени числителя (1>0).
Пример 28 Вычислить предел последовательности
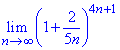
Решение: Задание следует свести под правило второго замечательного предела. Для этого в показателе создаем число, которое является обратно пропорциональным слагаемому возле единички в скобках.
Постоянный множитель при этом и будет показателем экспоненты в пределе
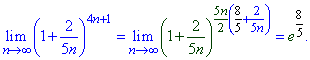
Пример 29 Найти лимит последовательности
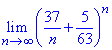
Решение: Поскольку оба значения в скобках меньше единицы (особенно важно 5/63<1), а одно из них, что зависит от номера, стремится к нулю, то их сумма в степени (n) также стремится к нулю
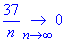
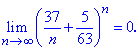
Пример 30. Известно, что лимит последовательности равен 13
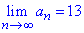
Найти следующий предел
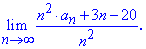
Решение: Выделим в числителе и знаменателе слагаемое, которое вносит наибольший вклад в предел и разделим на него
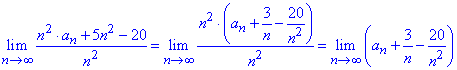
Слагаемые 3/n, -20/n^2 стремятся к нулю при номере стремящемся к бесконечности, поэтому предел равен
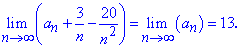
Пример 31 Вычислить предел функции
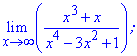
Решение Выделим слагаемое с самым большим показателем и разделим на него

Лимит равен нулю, поскольку степень переменной в знаменателе больше, чем в числителе.
Пример 32 Найти лимит функции

Решение При подстановке единицы в дробь получим неопределенность вида {0/0} .
Чтобы раскрыть неопределенность, выделим в числителе и знаменателе множитель, который пропорционален (x-1) .
Для этого разделим полиномы на указанный множитель.
В результате получим

Далее вносим разложение полиномов в предел и упрощаем

Пример 33 Найти предел функций
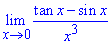
Решение Для раскрытия неопределенности {0/0} воспользуемся эквивалентными бесконечно малыми функциями.
Для этого запишем по два члена разложения tan(x), sin(x) в ряд Тейлора (одного недостаточно, в числителе получим 0)
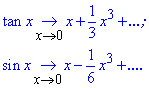
Далее подставим разложения в предел
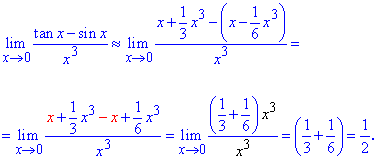
Переменная в кубе упростится и останутся числа, сумма которых и является искомым пределом.
Пример 34 Вычислить предел функции
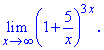
Решение Сведем под правило второго замечательного предела
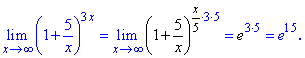
Задача простая, поэтому здесь не на чем останавливаться.
Больше ответов на пределы ищите на страницах сайта.
В каждой публикации разжевываем методику вычислений до элементарных мелочей, при таких объяснениях каждый студент может без проблем решить подобные примеры.
Однако дальше от студентов поступают новые заказы с просьбой найти предел.
Порой нужно помочь с простыми функциями, что составляет впечатление что студенты имеют худшую подготовку, чем ученики в 11 классе, которые изучают эту тему.
Пример 11. Вычислить предел последовательности:
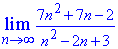
Решение: Подстановка большого номера в последовательность дает особенность вида бесконечность разделить на бесконечность. Для ее раскрытия в числителе и знаменателе дроби выделяем слагаемое, что вносит наибольший вклад. В скобках останутся константы + слагаемые, которые стремятся к нулю.
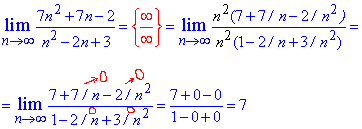
На общий множитель упрощаем, а константы дают значение предела последовательности.
Пример 12. Найти предел последовательности:
Решение: В предельном переходе имеем неопределенность вида бесконечность минус бесконечность. Функция представлена разницей корней. Чтобы избавиться от неопределенности, умножим и поделим разницу на сумму корней (сопряженное выражение). В результате придем к неопределенности бесконечность разделить на бесконечность. Чтобы ее раскрыть выносим множитель, что вносит наибольший вклад из числителя и знаменателя и сокращаем на него. Все что останется и будет пределом последовательности
Пример 13. Найти предел функции
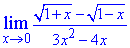
Решение: При переменной стремящейся к нулю имеем неопределенность {0/0}. Для ее раскрытия разницу корней умножим и разделим на сопряженное выражение, чтобы в числителе образовать разность квадратов. В знаменателе имеем полином, который содержит особенность, поэтому разложим его на простые множители. После упрощений получим зависимость, предел которой легко находим методом подстановки
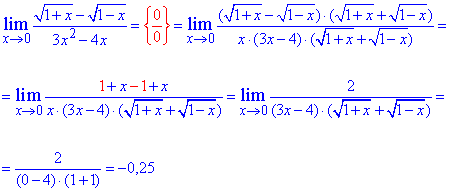
Пример 14. Вычислить предел
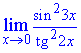
Решение: Переменная стремится к нулю, а функция задана долей синуса и тангенса в квадрате. В таких случаях нужно преобразовать выражение, чтобы в нем можно было легко выделить первый замечательный предел и его следствие. Для компенсации изменений в числитель и знаменатель записываем соответствующие константы. Далее переходим к произведению известных границ, вклад от каждой из которых равен единице.
Пример 15. Определить предел функции
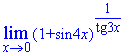
Решение: При переменной стремящейся к нулю получим неопределенность вида единица в степени бесконечность. Для ее раскрытия выразим в степени множитель, который обратно пропорционален sin(4x).
Таким образом получим второй замечательный предел – экспоненту, а все что останется в показателе, даст степень экспоненты. Но здесь имеем долю sin(4x)/tan(3x), поэтому переходим к лимиту в показателе, а сам показатель сводим к первому замечательному пределу его следствии.
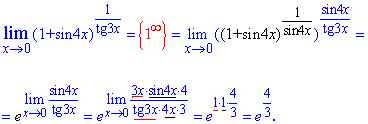
Из последнего «лимита» можно вывести простую формулу, которая может быть рассмотрена как следствие первого замечательного предела. Лимит доли тангенса к синусу (или наоборот) ровен доле их аргументов.
Пример 16. Найти предел последовательности:
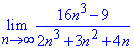
Решение: Для раскрытия особенности вида бесконечность разделить на бесконечность необходимо три раза применить правило Лопиталя. Другая схема заключается в вынесении из числителя и знаменателя наибольшего множителя, и сокращении на него. В результате останутся константы и бесконечно малые функции. Последние стремятся к нулю, поэтому лимит последовательности равен
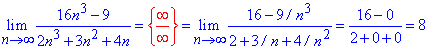
Пример 17. Вычислить предел последовательности:
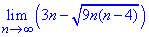
Решение: Таких лимитов в предыдущих публикациях вычислено немало и суть раскрытия подобных неопределенностей заключается в умножении на сопряженное выражение – сумму корней. На это же выражение следует разделить функцию, чтобы не изменить значение лимита. В результате в числителе дроби получим разность квадратов и таким образом избавляемся от иррациональности, а предел выражения получим через оценку максимальных множителей.
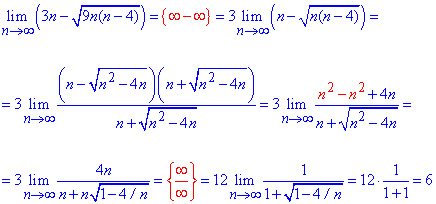
Пример 18. Определить лимит функции
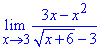
Решение: Когда переменная стремится к 3 имеем неопределенность вида {0/0}. Для раскрытия неопределенности в знаменателе дроби избавляемся от иррациональности умножением на сопряженное выражение, а в числителе полином раскладываем на простые множители. В результате и тат и там получаем выражение (х-3), на которое упрощаем.
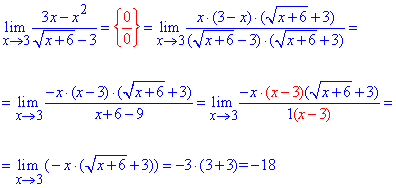
Лимит функции, что осталась, вычисляем методом подстановки.
Пример 19. Найти предел функции
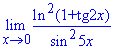
Решение: Предел функции в нуле дает особенность {0/0}. Ее не так просто раскрывать, как предыдущие.
Здесь следует свести выражение к первому и второму замечательному пределу и их следствиям.
Ln(1+x)/x в предельном переходе даст единицу, так же как и tan(x)/x и sin(x)/x.
Число 4/25 и будет лимитом функции.
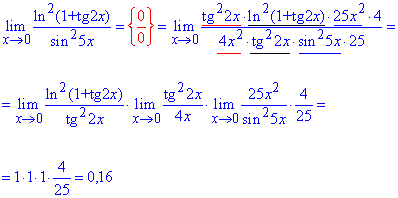
Пример 20. Найти лимит
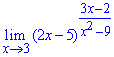
Решение: Предел функции в точке имеет неопределенность вида единица в степени бесконечность. Для ее раскрытия нужно преобразовать функцию под второй замечательный предел. Для этого и в скобках, и в показателе выделяем множитель, что вносит особенность (x-3) и делаем замену переменных t=x-3.
Далее переходим к экспоненте, и определяем лимит показательной функции.
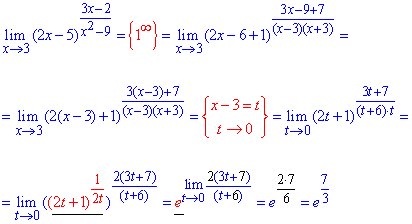
Как Вы могли убедиться, задания на пределы не самые сложные в высшей математике.
Нужно знать не так много правил, чтобы без труда находить правильный ответ.
Метод логарифмирования раскрытия неопределенностей в пределах
Пример 16 Вычислить предел по формуле Лопиталя limit(x^(1/(1-x)),x→0)
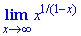
Решение: Предел имеет особенность типа 1^∞. Для применения метода логарифмирования за новую функцию обозначим y=x1/(1-x). Делее логарифмируем обе части, получим
ln(y)=ln(x1/(1-x))=ln(x)/(1-x).
По правилу Лопиталя раскрываем неопределенность вида 0/0
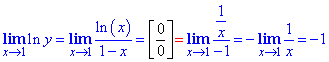
Это еще не конечный ответ, чтобы найти y нужно экспоненту поднести к степени равному найденному пределу.
ln(y)=-1 →y=e-1=1/e.
Пример 17 Раскрыть неопределенность по правилу Лопиталя

Решение: Имеем неопределенность типа ноль в степени ноль 0^0. Поступаем по схеме для показательных функций, а именно – логарифмуємо выражение в лимите.
y=(arcsin(x))2;
ln(y)=2x•ln(arcsin(x)).
Для раскрытия неопределенности используем правило Лопиталя дважды
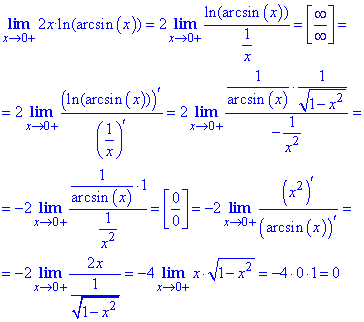
Здесь нужно брать производную от ln(arcsin(x)), как от сложной функции, помните об этом.
Пример 18 Найти предел пользуясь правилом Лопиталя
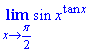
Решение: Подставки аргумента равного 90 градусам дает неопределенность вида единицы в степени бесконечность 1^∞. Согласно алгоритму вычисления пределов, функцию под лимитом следует прологарифмирувать. Далее найти предел логарифма, а потом экспонента в степени полученного значения и будет ответом к заданию. Проведем вычисления
y= tan(x)sin(x);
ln(y)=ln(sin(x))^tg(x)=tan(x)•ln(sin(x)).
Воспользуемся правилом Лопиталя, предварительно заменив тангенс на котангенс по формуле tg(x)=1/cot(x).
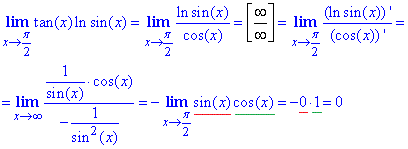
Но это еще не ответ, нужно потенцировать 0.
ln(y)=0 →y=e0=e.
Сведение неопределенностей в пределах под правило Лопиталя
Пример 19 Мнимая подстановка x=2 в функцию дает неопределенность вида 0/0, поэтому применяем правило Лопиталя однократно, а далее без труда вычисляем лимит.
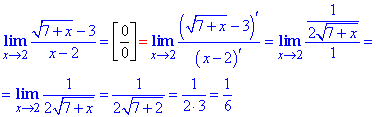
Пример 20 Подстановкой убеждаемся, что имеем неопределенность вида 0/0. По формуле Лопиталя вычисляем производную числителя и знаменателя по переменной, чтобы раскрыть неопределенность.
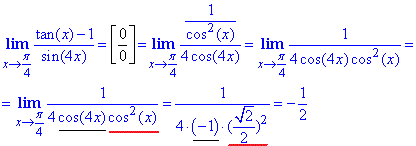
Пример 21 Имеем долю полиномов без свободного члена, что в предельной точке дает особенность вида 0/0. Для ее раскрытие по правилу Лопиталя дифференцируем каждый полином пока не получим дробь, предел которой можно вычислить подстановкой
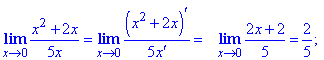
Пример 22 В числителе имеем x^2, в знаменателе 2^x.
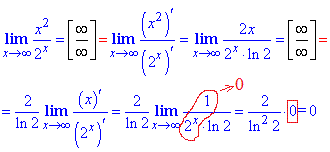
Решение: Поскольку аргумент стремится к бесконечности, то прямая подстановка дает особенность вида ∞/∞. Ее раскрываем дважды беря производные числителя и знаменателя по "x".
Пример 23 Имеем дробь с функций e^x, x^a. В такого сорта примерах правило Лопиталя применяют до тех пор, пока в знаменателе не получим факториал числа a!
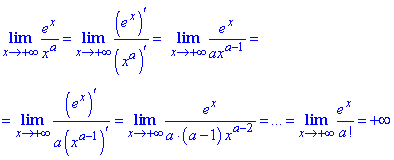
Запомните, что ограничений на количество повторных применений правила Лопиталя нет, находим производные до тех пор, пока имеем одну из неопределенностей 0/0 или ∞/∞.
Пример 24 Очередное задание на раскрытие неопределенности вида ∞/∞ решаем путем дифференцирования отдельно числителя x^a и знаменателя ln(x).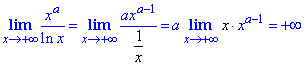
Пример 25 Имеем долю функций f(x)=arctan(x) и g(x)=e3x-1. В нуле они дают неопределенность вида 0/0, поэтому имеем все основания применить правило Лопиталя.
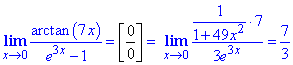
Поскольку выражения e^3x→1 и 1/(1+49x^2) →1 когда x→0, то предел равен 7/3.
Пример 26 Согласно алгоритму, чтобы раскрыть неопределенность ∞/∞ дважды применяем правило Лопиталя.
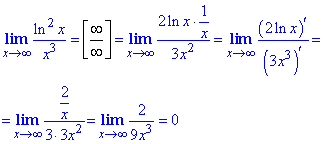
Пример 27 Переходим от неопределенности вида ноль умножить на бесконечность к неопределенности бесконечность разделить на бесконечность, которую раскрываем по правилу Лопиталя через дифференцирование числителя и знаменателя дроби. Внимательно посмотрите схему перехода от одной неопределенности к другой и запомните, что когда имеем произведение логарифма на другую функцию, то в знаменатель переносим последнюю, а не логарифм.
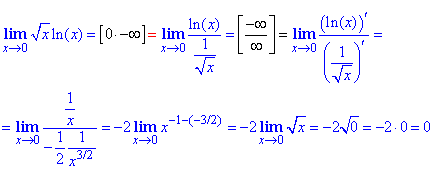
Пример 28 Прямая подстановка дает неопределенность ноль умножить на бесконечность 0*∞
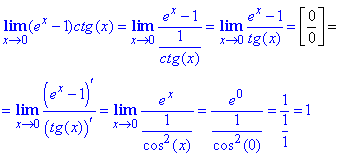
Чтобы свести пример к применению правила Лопиталя в искусственный способ котангенс переносим в знаменатель дроби, а далее заменяем 1/ctg(x)=tg(x). Таким образом получаем особенность в виде доли бесконечно малых функций, раскрываем дифференцированием по Лопиталю и подстановкой x=0.
Раскрытие неопределенностей ∞-∞
Пределы с неопределенностью ∞-∞ также раскрываем по правилу Лопиталя, но предварительно проводим определенные элементарные действия над слагаемыми, чтобы перейти от разности бесконечно больших функций к дроби.
Пример 29 Формулы ниже хорошо иллюстрируют как дважды применяли дифференцирование числителя и знаменателя дроби, чтобы избавиться от неопределенности 0/0.
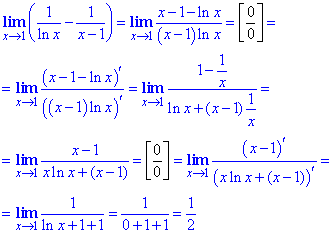
Пример 30 Имеем неопределенность вида ∞-∞, которую раскрываем путем сведения дробей к общему знаменателю. Далее по правилу Лопиталя вычисляем производные числителя и знаменателя, и так дважды.
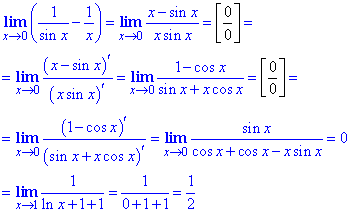
И только когда избавляемся неопределенности выполняем подстановку аргумента в предел. Считаем, чтобы начать решать примеры на правило Лопиталя, 30 приведенных примеров вполне достаточно. Если есть проблемы с расчетными или модулями, то всегда можете обращаться к нам за помощью!
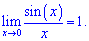
Последствия первого замечательного предела
Стоит отметить, что не все пределы, содержащие тригонометрические функции следует сразу сводить к первому замечательному пределу. Все зависит, как входит функция, и можно ли свести под нужную формулу. Плюс тригонометрические функции, когда те стремятся к нулю всегда можно заменить эквивалентными бесконечно малыми выражениями, но это уже другая техника вычисления пределов.
что стремится к нулю. Об этом Вы должны помнить и только в таких случаях сводить вычисления под правило первого замечательного предела. Важно чтобы переменная в тригонометрической функции стремилась к нулю, например:
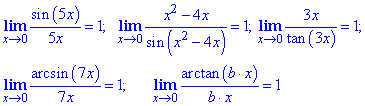
В следующих пределах все аргументы тригонометрических функций стремятся к нулю.
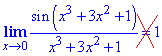
У Вас возникнет вопрос, Почему так? А потому что выражение x3+3x^2+1 не стремится к нулю, когда переменная x стремится к нулю.
Попробуйте самостоятельно найти предложенный предел, а мы в конце статьи сверим ответы.
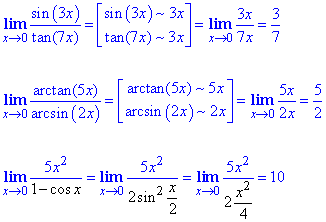
что есть правильно, целесообразно и оправдано в плане времени затраченного на расчеты.
Но сейчас у нас задача, научить Вас решать задачи на первый предел, поэтому переходим к подготовленных ответов.
Примеры на первый замечательный предел
Пример 1 Найти лимит 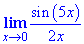
Вычисления: Если видите в пределе синус, то из этого не всегда следует о необходимости сводить к первому замечательному пределу.
Сначала подставим 0 в выражение под знаком лимита (делаем это в голове не записывая в тетрадь, или можете записать какую особенность получили):
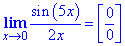
Итак, имеем особенность типа 0/0, ее можно указать при разборе, все зависит от Вуза и требований к оформлению ответов. Дробь под знаком предела похож на первый замечательный предел, но это не он.
Для сведения под формулу первого замечательного предела необходимо в искусственный способ в знаменателе получить такое же выражение, которое имеем под синусом.
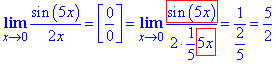
Обведенное выражение у нас равно первому пределу, все остальные — множитель при ней.
Аналогично получите если заменить синус эквивалентным бесконечно малым значением sin(5x)~5x.
Ответ: 5/2.
Пример 2 Вычислить предел дроби
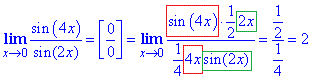
Вычисления: Числитель и знаменатель умножили на переменную, а далее искусственно ввели множители которые фигурируют как аргументы синусов. Таким образом получили две замечательные пределы и множители, которые в конце упростили.
Ответ: 5/2.
Пример 3 Найти предел
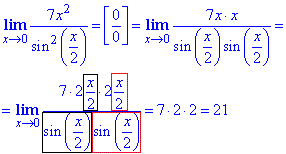
Вычисления: Здесь искусственно возвели выражение в числителе под аргумент синуса и выразили первый замечательный предел, после этого вычисления упростились до умножения трех чисел.
Ответ:21.
Пример 4 Найти предел
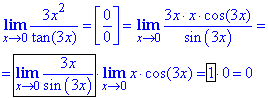
Вычисления: Простая подстановка показывает, что имеем неопределенность вида 0/0, которую нужно раскрыть. Распишем в знаменателе tan(3x) по тригонометрической формуле tan(3x)=sin(3x)/cos(3x), а в числителе выделим множитель 3x. Таким образом получим первый важный предел умноженный на предел от x•cos(3x), который равен нулю.
Здесь не пришлось искать дополнительные множители, однако раскрытие неопределенности показало, что можно получить в результате как нуль, так и бесконечность, если бы имели обратное выражение.
Ответ:0.
Пример 5 Вычислить предел
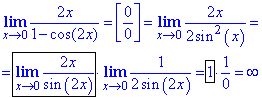
Вычисления: Неопределенность типа 0/0 раскрываем путем выделения первого замечательного предела, только на этот раз выражение, что остается во втором пределе стремится к бесконечности при переменной стремящейся к нулю.
Здесь использовали тригонометрическую формулу
1-cos(2x)=2sin2(x).
Ответ: ∞.
Бывают примеры когда применение эквивалентных бесконечно малых величин является более эффективным в плане простоты вычислений, чем возведение под первый предел.
Пример 6 Найти предел
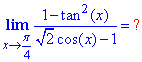
Вычисления: Легко убедиться, что числитель и знаменатель стремятся к нулю. Для нахождения предела используем разложение функций cos(x), tan2(x) по степеням при x→π/4.
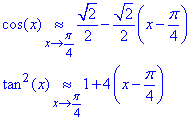
Подставим полученные значения в предел
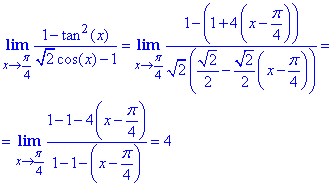
Ответ:4.
Пример 7 Найти предел
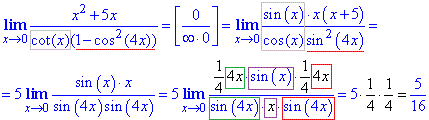
Вычисления: Здесь сot(х) расписали по формуле ctg(x)=cos(x)/sin(x). Далее упростили слагаемые, которые не вносят вклада в предел. И напоследок в числителе и знаменателе ввели множители, которые позволили в одном примере выделить три замечательных предела. Все остальные константы после умножения дали значение предела.
Ответ: 5/16.
Пример 8 Найти предел функции
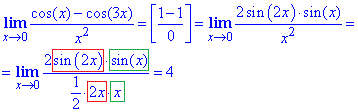
Вычисление: Получили несколько иную неопределенность от рассмотренных ранее, которую раскрыли с помощью тригонометрической формулы
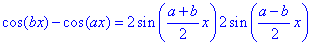
В результате получили произведение двух первых важных пределов.
Ответ: 4.
Пример 9 Вычислить лимит
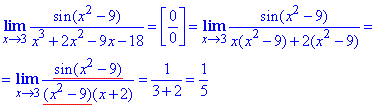
Вычисление Раскрыть неопределенность типа 0/0 удалось благодаря выделению в знаменателе множителя, который фигурирует в качестве аргумента синуса в числителе дроби. Здесь можно было выполнить замену переменных y = x-3 , что вы можете проверить самостоятельно и подобным образом свести решение к первому важному пределу.
Ответ: 1/5.
Пример 10 Вычислить предел функции
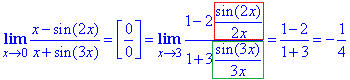
Вычисление Подстановка 0 показывает, что у нас неопределенность 0/ 0, которую необходимо раскрыть. Чтобы свести дробь под первую особую границу в числителе и знаменателе выносим аргумент и добиваемся, чтобы дроби, содержащий синусы имели в знаменателе одинаковые аргументы как в синусах.
Ответ: - 1/4.
Пример 11 Вычислить предел
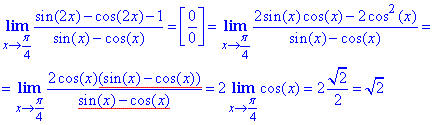
Здесь использовали тригонометрические формулы синуса двойного угла sin(2x)=2sin(x)cos(x) и зависимость 1+cos(2x)=2cos2(x)
Ответ: √2.
Пример 12 Вычислить предел
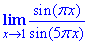
Решение: Первый замечательный предел здесь применять напрямую нельзя, поскольку аргументы πx, 5πx не стремятся к нулю при x→1. Поэтому необходимо выполнить замену переменных x-1=y, тогда при x→1 переменная y→0, что и необходимо для применения 1 замечательного предела. Далее учли периодичность тригонометрических функций и искусственно ввели нужные множители
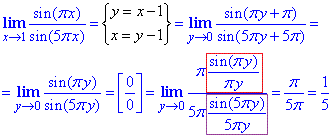
Ответ: 1/5.
Пример 13 Вычислить предел
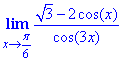
Решение: Вводим замену переменных x-π/6=y, далее расписав функции используем тригонометрическую форму представления разности косинусов через произведение соответствующих синусов. Остальные вычислений заключается в выделении первого важного предела
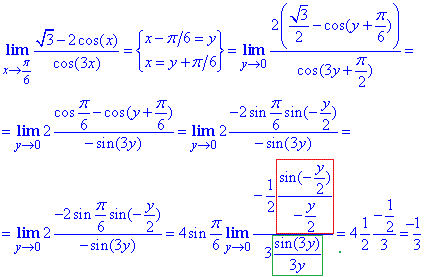
Ответ: -1/3.
Пример 14 Найти лимит функции
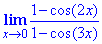
Решение: Поскольку, взятые отдельно пределы числителя 1-cos(2x) и знаменателя 1-cos(3x) стремятся к нулю когда x стремится к нулю, то имеем особенность типа нуль разделить на нуль. Раскроем неопределенность посредством сведения к первому замечательному пределу. Для этого используем следующие тригонометрические формулы, чтоб, перейти от косинусов к синусам
1-cos(2x)=2sin2(x);
1-cos(3x)=2sin2(3x/2).
С учетом формул выше, вычислим предел функции
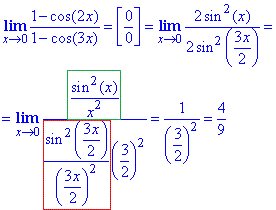
Ответ: 4/9.
Пример 15 Найти лимит функции
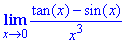
Решение: Подстановка в уме аргумента равного нулю в числитель и знаменатель дает особенность типа нуль разделить на нуль 0/0. Для раскрыияь неопределенности распишем тангенс, а дальше с помощью тригонометрических формул заменим 1-cos(x)=2sin2(x/2). Далее искусственным введением необходимого множителя сведём под правило первого замечательного предела.
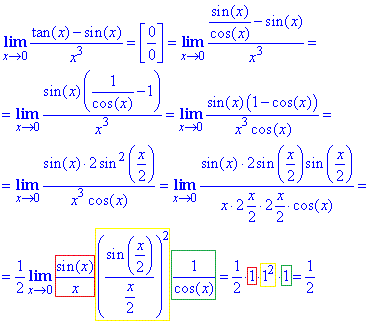
Ответ: 1/2.
При вычислениях Вам часто приходится использовать различные тригонометрические формулы, которые позволяют перейти к синусам. Мы для Вас их сгруппировали, можете скопировать, распечатать и использовать в обучении.
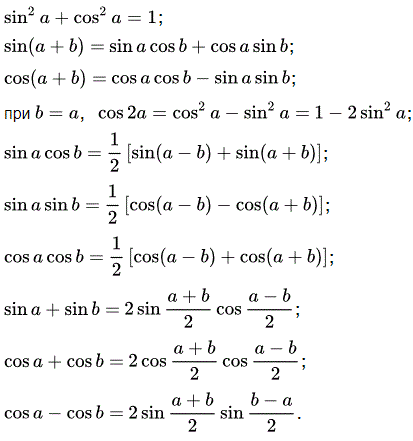
И в начале мы говорили что предел 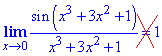 подобный первому пределу, но не равен 1, потому что аргумент не стремится к нулю. Если подставить нуль в числитель и знаменатель, то получим limit=sin(1). Если Вы к этому пришли самостоятельно, и можете решать приведённые примеры без помощи, то практикумы и экзамены сдадите на отлично.
подобный первому пределу, но не равен 1, потому что аргумент не стремится к нулю. Если подставить нуль в числитель и знаменатель, то получим limit=sin(1). Если Вы к этому пришли самостоятельно, и можете решать приведённые примеры без помощи, то практикумы и экзамены сдадите на отлично.
На этом решение примеров на первую важную границу не заканчивается, больше готовых ответов Вы можете найти на соседних страницах сайта.
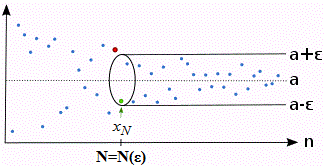
Если a является пределом последовательности то этому соответствует запись
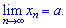
Вычисление предела числовой последовательности
Пример 1 Легкое задание, которое учит выносить доминантные множители в дробях, которые дают наибольший вклад при номере, стремлящемся к бесконечности, и упрощать на них
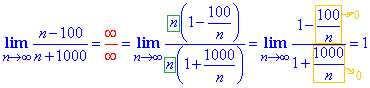
В этом вся сложность алгоритма вычисления предела последовательности при переменной стремящейся к бесконечности, но бывают исключения, о которых поговорим делее.
Если последовательность сходится, то она имеет конечный лимит. Если предел равен бесконечности, то говорят, что такая последовательность расходится.
Для установления сходимости последовательностей нужно хорошо уметь находить пределі, что мы с Вами постоянно совершенствуем.
Пример 2 Имеем неопределенность вида бесконечность минус бесконечность (∞-∞), поэтому теорему о разнице пределов здесь применять нельзя. Преобразуем выражение, умножением и делением на сопряженное выражение. Для вычисления значения предела упрощаем дробь на выражение, что вносит наибольший вклад при аргументе стемящемся к бесконечности. Как выносить множители из под корня Вы должны научиться самостоятельно, без этого трудно будет раскрывать пределы с корнями.
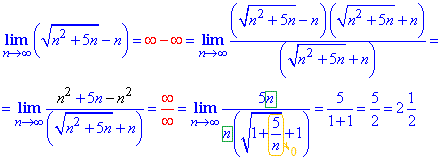
Пример 3 Разницу корней в знаменателе дроби не уножаєм на сопряженное выражение, а просто номер n выносим из под корня (внимательно посмотрите как это делать), а дальше упрощаем с n выделенным в числителе
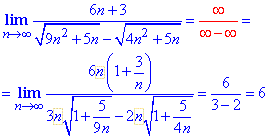
Пример 4 Последовательность из частки иррациональных выражений имеет конечную границу, если степень номера n в знаменателе равен степени в числителе (или больше). Его выделяем по указанной в методике формуле, и упрощаем
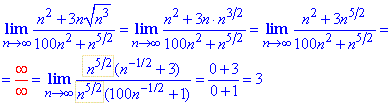
Пример 5 Найти предел последовательности 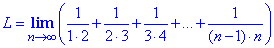
Вычисления: Проанализировав, как меняются слагаемые для всех номеров k=2,3,4 можем записать формулу
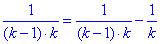
Таким образом исходную сумму сводим к виду
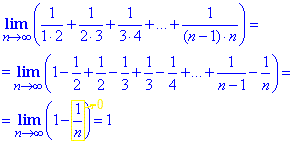
Единого устоявшегося алгоритма, как раскрывать такие суммы нет. Порой можно увидеть простые схемы чередования слагаемых, в других заданиях бывает нужно вычислить суммы арифметических или геометрических прогрессий. Лишь бы оценить сверху, что последовательность ограничена, и к какому значению стремится.
Пример 6 Лимит последовательности из частки показательных выражений вычисляют путем выделения и упрощения доминантных множителей в числителе и знаменателе дроби. В заданном лимите основания равны 2 и 4, их можно свести к общему 4 в (высшем) степени ровному n. Все остальное и даст значение к которому стремится дробь.
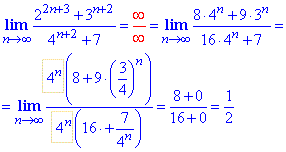
Пример 7 Предел последовательности из разности бесконечно больших дробей раскрываем методом сведения их к общему знаменателю и упрощения в числителе и знаменателе множителя, что вносит главный вклад
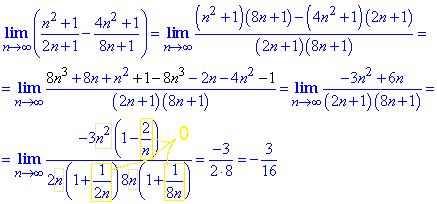
Пример 8 Найти лимит последовательности
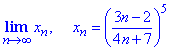
Вычисления: Представим общий член последовательности {xn} в виде
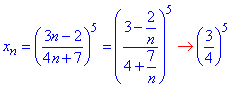
По теореме о границе показательной функции, она равна показателю от границы основы, если степень конечна. Отсюда lim{xn}=(3/4)^5.
Пример 9 В такого сорта заданиях вынесения n в главной степени за скобки в числителе и знаменателе дроби к упрощению не приведет. Попробуйте проверить самостоятельно, остается взглянуть в формулы сокращенного умножения и расписать разницы и суммы в кубе и в четвертой степени по следующим формулам
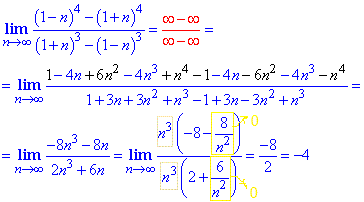
Таким образом, получим слагаемые с противоположными знаками, которые в сумме дадут 0, остальные слагаемые в предельном переходе упростятся по приведенной выше методике.
И напоследок, еще несколько решений на предел последовательности, которые предлагаем разобрать самостоятельно.
10 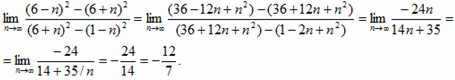
11 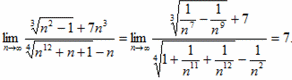
12 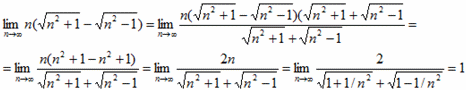
13 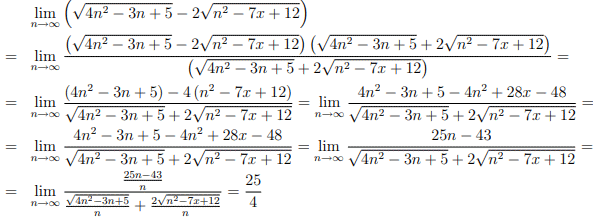
Пример 35. Имеем последовательность в виде дроби, где в числителе и знаменателе находятся корневые функции.
Нужно найти предел при номере стремящемся к бесконечности.
Здесь раскрывать иррациональности в числителе не нужно, а только внимательно проанализировать корни и найти где содержится более высокая степень номера.
В первом корни числителя имеем множителем n^4, то есть n^2 можем вынести за скобки.
Тоже самое проделаем со знаменателем.
Далее оцениваем значение подкоренных выражений при предельном переходе.
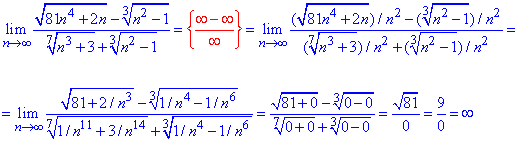
Получили деления на ноль, что является неправильно в школьном курсе, но в предельном переходе это допустимо.
Только с поправкой, "чтобы оценить куда стремится функция".
Поэтому приведенную запись не все преподаватели могут трактовать правильной, хотя и понимают, что результирующий преде от этого не изменится.
Давайте рассмотрим ответ, составленный по требованиям преподавателей согласно теорией.
Для упрощения оценим только главные доданки под корнем
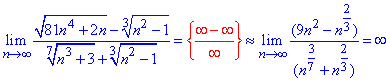
Далее в числителе степень равен 2, в знаменателе 2/3, следовательно числитель быстрее растет, а значит предел стремится к бесконечности.
Его знак зависит от множителей при n^2, n^(2/3), поэтому он положительный.
Пример 36.Рассмотрим пример предела на деление показательных функций. Таких примеров на практических рассматривается мало, поэтому не все студенты с легкостью видят, как раскрывать неопределенности, что возникают.
Максимальный множитель для числителя и знаменателя равен 8^n, на него и упрощаем
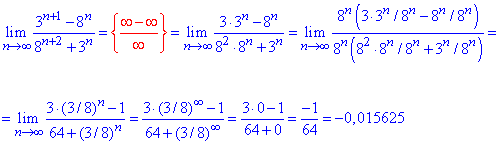 Далее оцениваем вклад каждого слагаемого
Далее оцениваем вклад каждого слагаемого
Слагаемые 3/8 стремятся к нулю 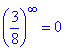 при переменной направляюейся к бесконечности, поскольку 3/8<1 (свойство степенно-показательной функции).
при переменной направляюейся к бесконечности, поскольку 3/8<1 (свойство степенно-показательной функции).
Пример 37.Предел последовательности с факториалами раскрывается розписанням факториала к наибольшему общему множителю для числителя и знаменателя.
Далее на него сокращаем и оцениваем лимит по значению показателей номера в числителе и знаменателе.
В нашем примере знаменатель быстрее растет, поэтому предел равен нулю.
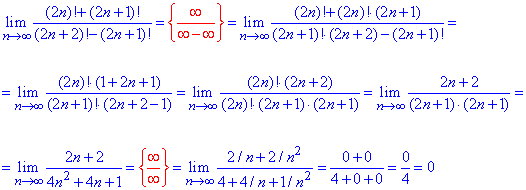
Здесь использована следующее
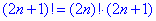
свойство факториала.
Пример 38.Не применяя правила Лопиталя сравниваем максимальные показатели переменной в числителе и знаменателе дроби.
Так как знаменатель содержит старший показатель переменной 4>2 то и растет он быстрее.
Отсюда делаем вывод, что предел функции стремится к нулю.
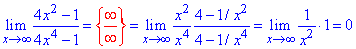
Пример 39.Раскрываем особенность вида бесконечность разделить на бесконечность методом вынесения x^4 с числителя и знаменателя дроби.
В результате предельного перехода получим бесконечность.
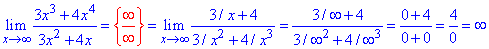
Пример 40. Имеем деление полиномов, нужно определить предел при переменной стремящейся к бесконечности.
Старший степень переменной в числителе и знаменателе равен 3, это значит что граница существует и равна сталой.
Вынесем x^3 и выполним предельный переход
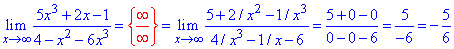
Пример 41.Имеем особенность типа единица в степени бесконечность.
А это значит, что выражение в скобках и сам показатель надо свести под вторую важную границу.
Распишем числитель, чтобы выделить в нем выражение идентичное знаменателе.
Далее переходим к выражению, содержащем единицу плюс слагаемое.
В степени нужно выделить множителем 1/(слагаемое).
Таким образом получим экспоненту в степени предела дробной функции.
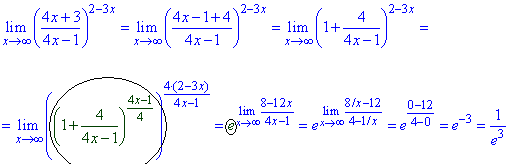 Для раскрития особенности использовали второй предел:
Для раскрития особенности использовали второй предел:
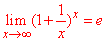
Пример 42.Имеем особенность типа единица в степени бесконечность.
Для ее раскрытия следует свести функцию под второй замечатеьный предел.
Как это сделать подробно показано в приведенной далее формуле
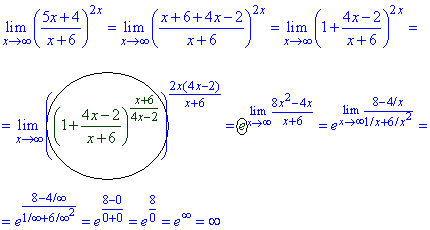
Подобных задач Вы можете найти очень много. Их суть в том, чтобы в показателе получить нужный степень, а он равен обратному значению слагаемого в скобках при единицы.
Таким методом получаем экспоненту. Дальнейшее вычисление сводится к вичислению предела степени экспоненты.
Здесь экспоненциальная функция стремится к бесконечности 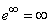 , поскольку значение больше единицы e=2.72>1.
, поскольку значение больше единицы e=2.72>1.
Пример 43 В знаменателе дроби имеем неопределенность типа бесконечность минус бесконечность, фактически равное делению на ноль.
Чтобы избавиться корня домножим на сопряженное выражение, а дальше по формуле разности квадратов перепишем знаменатель.
Получим неопределенность бесконечность разделить на бесконечность, поэтому выносим переменную в наибольшей степени и сокращаем на нее.
Далее оцениваем вклад каждого слагаемого и находим предел функции на бесконечности
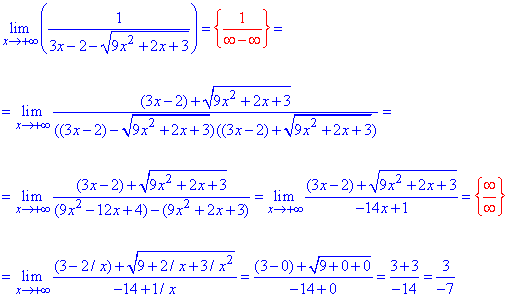
Пример 44.Найти повторные границы
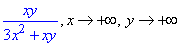
Решение: Вычисляем предел функции двух переменных сначала по y, а дальше – x)
a)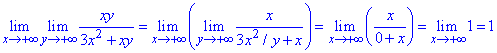
б) 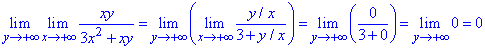
Пример 45. Вычислить повторные границы
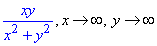
Решение: Методика вычисления повторных границ не сложна:
сначала находим границу по одной переменной, считая вторую переменную постоянной.
Далее остается функция от одной переменной, а таких пределов мы разобрали очень много.
а) 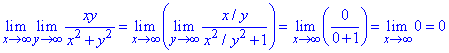
б) 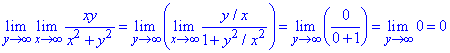
В этом задании предел по первой переменной равен нулю, поэтому повторные записываем только для формальности.
Предел в данном случае от порядка нахождения не зависит.
Однако, если взглянуть ответ из предыдущего примера то такое утверждение не всегда выполняется.
Ищите эффективные схемы вычисления пределов на страницах сайта, если возникают проблемы с пределами на экзаменах и модулях - обращайтесь за помощью!
]]>Далее остановимся и проанализируем пределы с неопределенностями, методы раскрытия неопределенностей, применением первой и второй важных границ и их последствий.
Приведенные примеры полностью не охватят всей темы, но на многие вопросы внесут ясность.
Найти предел функции в точке:
Пример 46. Предел функции в точке определяем подстановкой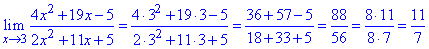
Так как знаменатель дроби не превращается в ноль то такую задача под силу решить каждому выпускнику школы.
Пример 47. Имеем долю полиномов, кроме того знаменатель не содержит особенности (не равен нулю).
Еще одна задача, фактически за 11 класс.
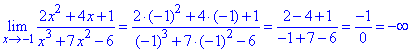
Пример 48. Методом подстановки определяем предел функции
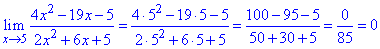 Из условия следует, что граница функции равна двум, если переменная стремится к бесконечности.
Из условия следует, что граница функции равна двум, если переменная стремится к бесконечности.
Пример 49.Прямая подстановка x=2 показывает, что граница в точке имеет особенность {0/0}. Это означает, что и числитель и знаменатель скрыто содержат (x-2).
Выполняем разложение полиномов на простые множители, а потом сокращаем дробь на указанный множитель (x-2).
Предел дроби, которая останется, находим методом подстановки.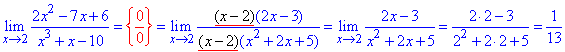
Пример 50.Предел функции в точке имеет особенность типа {0/0}.
Избавляемся разницы корней методом умножения на сумму корней (сопряженное выражение), полином раскладываем.
Далее, упростив функцию, находим значение предела в единице.
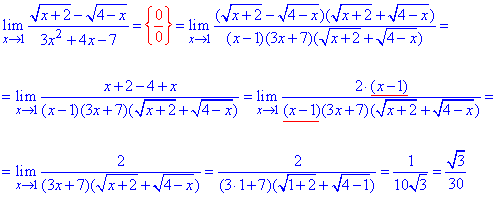
Пример 51.Рассмотрим задачу на сложные пределы.
До сих пор от иррациональности избавлялись методом умножения на сопряженное выражение.
Здесь же, в знаменателе, имеем корень кубический, поэтому нужно использовать формулу разности кубов.
Все остальные преобразования повторяются от условия к условию.
Полином раскладываем на простые множители,
далее сокращаем на множитель, который вносит особенность (0)
и подстановкой x=-3 находим предел функции в точке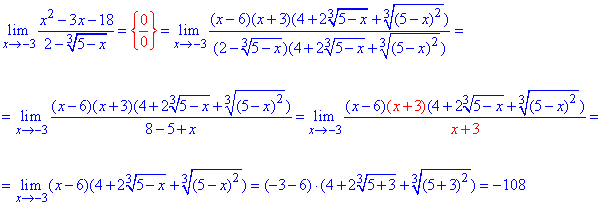
Пример 52.Особенность вида {0/0} раскрываем с помощью первого замечательного предела и его последствий.
Сначала разницу синусов распишем согласно тригонометрической формуле
sin(7x)-sin(3x)=2sin(2x)cos(5x).
Далее числитель и знаменатель дроби дополняем выражениями, которые необходимы для выделения важных пределов.
Переходим к произведению пределов и оцениваем вложение каждого множителя.
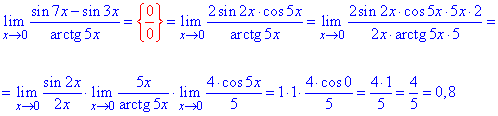
Здесь использовали первый замечательный предел:
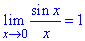
и следствия из него
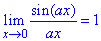
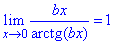
где a и b – произвольные числа.
Пример 53.Чтобы раскрыть неопределенность при переменной стремящейся к нулю, используем второй замечательный предел.
Чтобы выделить экспоненту, приводим показатель к 2-му замечательному пределу, а все остальное, что останется в предельном переходе, даст степень експоненты.
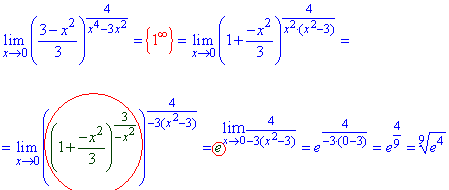
Здесь использовали следствие из второго замечатеьного предела:
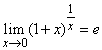
Вычислить предел функции в точке:
Пример 54. Нужно найти предел функции в точке. Простая подстановка значения показывает, что имеем деление нулей.
Для ее раскрытия разложим на простые множители полиномы и выполним сокращение на множитель, который вносит особенность (х+2).
Однако числитель дальше содержит (x+2), а это значит, что при x=-2 граница равна нулю.
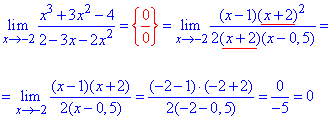
Пример 55.Имеем дробную функцию - в числителе разница корней, в знаменателе - поленом.
Прямая подстановка дает особенность вида {0/0}.
Переменная стремится к минус единице, а это значит, что следует искать и избавляться особенности вида (x+1).
Для этого избавляемся иррациональности умножением на сумму корней, а квадратичную функцию раскладываем на простые множители.
После всех сокращений методом подстановки определяем предел функции в точке
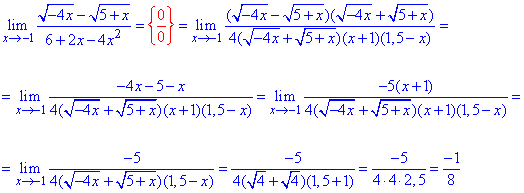
Пример 56.С виду подлимитной функции можно ошибочно заключить, что нужно применить первый предел, но вычисления показали, что все гораздо проще.
Сначала распишем сумму синусов в знаменателе sin(2x)+sin(6x)=2sin(4x)*cos(2x).
Далее расписываем tg(2x), и синус двойного угла sin(4x)=2sin(2x)cos (2x).
Синусы упрощаем и методом подстановки вычисляем предел дроби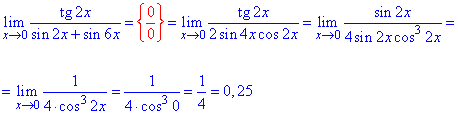
Пример 57.Задача на умение использовать вторую замечательный предел:
суть заключается в том, что следует выделить ту часть, которая дает экспоненту.
Остальное, что останется в показателе в предельном переходе даст степень экспоненты.
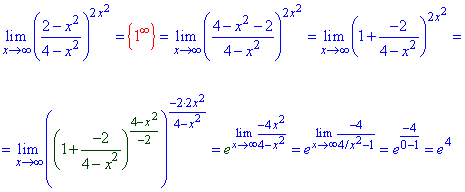
На этом разбор задач на пределы функций и последовательностей не заканчивается.
В настоящее время подготовлено более 150 готовых ответов к пределам функций, поэтому изучайте и делитесь ссылками на материалы с однокласниками.
Формула первого замечательного предела
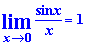 Следствия первого замечательного предела запишем формулами
Следствия первого замечательного предела запишем формулами
1. 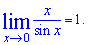 2.
2. 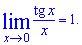 3.
3. 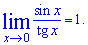 4.
4. 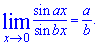 Но сами по себе общие формулы замечательных пределов никому на экзамене или тесте не помогают. Суть в том что реальные задания построены так что к записанным выше формулам нужно еще прийти. И большинство студентов, которые пропускают пары, заочно изучают этот курс или имеют преподавателей, которые сами не всегда понимают о чем объясняют, не могут вычислить самых элементарных примеров на замечательные пределы. Из формул первого замечательного предела видим, что с их помощью можно исследовать неопределенности типа ноль разделить на ноль
Но сами по себе общие формулы замечательных пределов никому на экзамене или тесте не помогают. Суть в том что реальные задания построены так что к записанным выше формулам нужно еще прийти. И большинство студентов, которые пропускают пары, заочно изучают этот курс или имеют преподавателей, которые сами не всегда понимают о чем объясняют, не могут вычислить самых элементарных примеров на замечательные пределы. Из формул первого замечательного предела видим, что с их помощью можно исследовать неопределенности типа ноль разделить на ноль  для выражений с тригонометрическими функциями. Рассмотрим сначала ряд примеров на первый замечательный пределу, а потом изучим второй замечательный предел.
для выражений с тригонометрическими функциями. Рассмотрим сначала ряд примеров на первый замечательный пределу, а потом изучим второй замечательный предел.
Пример 1. Найти предел функции sin(7*x)/(5*x)
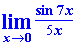 Решение: Как видите функция под пределом близка к первому замечательному пределу, но сам предел функции точно не равен единице. В такого рода заданиях на пределы следует в знаменателе выделить переменную с таким же коэффициентом, который содержится при переменной под синусом. В данном случае следует разделить и умножить на 7
Решение: Как видите функция под пределом близка к первому замечательному пределу, но сам предел функции точно не равен единице. В такого рода заданиях на пределы следует в знаменателе выделить переменную с таким же коэффициентом, который содержится при переменной под синусом. В данном случае следует разделить и умножить на 7
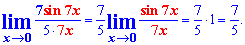
Некоторым такая детализация покажется лишней, но большинству студентов которым трудно даются пределы поможет лучше понять правила и усвоить теоретический материал.
Также, если есть обратный вид функции - это также первый замечательный предел. А все потому, что замечательный предел равен единице
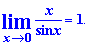
Это же правило касается и следствий 1 замечательного предела. Поэтому если Вас спросят "Чему равен первый замечательный предел?" Вы без колебаний должны ответить, что это - единица.
Пример 2. Найти предел функции sin(6x)/tan(11x)
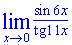 Решение: Для понимания конечного результата распишем функцию в виде
Решение: Для понимания конечного результата распишем функцию в виде
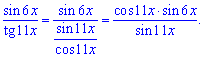
Чтобы применить правила замечательного предела умножим и разделим на множители
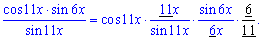
Далее предел произведения функций распишем через произведение пределов
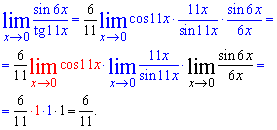
Без сложных формул мы нашли предел часки тригонометрических функций. Для усвоения простых формул попробуйте придумать и найти предел на 2 и 4 формулу следствия 1 замечательного предела. Мы рассмотрим более сложные задачи.
Пример 3. Вычислить предел (1-cos(x))/x^2
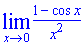 Решение: При проверке подстановкой получим неопределенность 0/0. Многим неизвестно, как свести такой пример до 1 замечательного предела. Здесь следует использовать тригонометрическую формулу
Решение: При проверке подстановкой получим неопределенность 0/0. Многим неизвестно, как свести такой пример до 1 замечательного предела. Здесь следует использовать тригонометрическую формулу
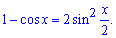
При этом предел преобразится к понятному виду
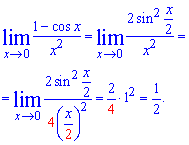
Нам удалось свести функцию к квадрату замечательного предела.
Пример 4. Найти предел
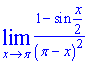 Решение: При подстановке получим знакомую особенность 0/0. Однако переменная стремится к Pi, а не к нулю. Поэтому для применения первого замечательного предела выполним такую замену переменной х, чтобы новая переменная направлялась к нулю. Для этого знаменатель обозначим за новую переменную Pi-x=y
Решение: При подстановке получим знакомую особенность 0/0. Однако переменная стремится к Pi, а не к нулю. Поэтому для применения первого замечательного предела выполним такую замену переменной х, чтобы новая переменная направлялась к нулю. Для этого знаменатель обозначим за новую переменную Pi-x=y
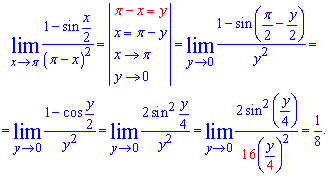
Таким образом использовав тригонометрическую формулу, которая приведена в предыдущем задании, пример сведен к 1 замечательному пределу.
Пример 5. Вычислить предел
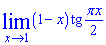 Решение: Сначала неясно как упростить пределы. Но раз есть пример, значит должен быть и ответ. То что переменная направляется к единице дает при подстановке особенность вида ноль умножить на бесконечность, поэтому тангенс нужно заменить по формуле
Решение: Сначала неясно как упростить пределы. Но раз есть пример, значит должен быть и ответ. То что переменная направляется к единице дает при подстановке особенность вида ноль умножить на бесконечность, поэтому тангенс нужно заменить по формуле
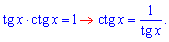
После этого получим нужную неопределенность 0/0. Далее выполняем замену переменных в пределе, и используем периодичность котангенса
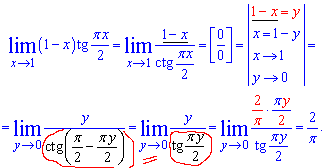
Последние замены позволяют использовать следствие 1 замечательного предела.
Второй замечательный предел равен экспоненте
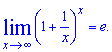 Это классика к которой в реальных задачах на пределы не всегда легко прийти.
Это классика к которой в реальных задачах на пределы не всегда легко прийти.
В вычислениях Вам понадобятся пределы - следствия второго замечательного предела:
1. 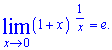 2.
2. 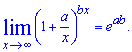 3.
3. 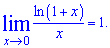 4.
4. 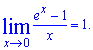
Благодаря второму замечательному пределу и его последствиям можно исследовать неопределенности типа ноль разделить на ноль, единица в степени бесконечность, и бесконечность разделить на бесконечность, да еще и в таком же степени
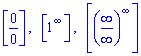
Начнем для ознакомления с простых примеров.
Пример 6. Найти предел функции
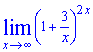 Решение: Напрямую применить 2 замечательный пределу не получится. Сначала следует превратить показатель, чтобы он имел вид обратный к слагаемому в скобках
Решение: Напрямую применить 2 замечательный пределу не получится. Сначала следует превратить показатель, чтобы он имел вид обратный к слагаемому в скобках
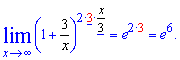
Это и есть техника сведения к 2 замечательному пределу и по сути - вывода 2 формулы следствия предела.
Пример 7. Найти предел функции
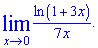 Решение: Имеем задания на 3 формулу следствия 2 замечательного предела. Подстановка нуля дает особенность вида 0/0. Для возведения предела под правило превратим знаменатель, чтоб при переменной был тот же коэффициент что и в логарифм
Решение: Имеем задания на 3 формулу следствия 2 замечательного предела. Подстановка нуля дает особенность вида 0/0. Для возведения предела под правило превратим знаменатель, чтоб при переменной был тот же коэффициент что и в логарифм
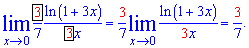
Это также легко понять и выполнить на экзамене. Трудности у студентов при исчислении пределов начинаются с следующих задач.
Пример 8. Вычислить предел функции [(x+7)/(x-3)]^(x-2)
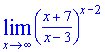 Решение: Имеем особенность типа 1 в степени бесконечность. Если не верите, можете везде вместо "икс" подставить бесконечность и убедиться в этом. Для возведения под правило поделим в скобках числитель на знаменатель, для этого предварительно выполним манипуляции
Решение: Имеем особенность типа 1 в степени бесконечность. Если не верите, можете везде вместо "икс" подставить бесконечность и убедиться в этом. Для возведения под правило поделим в скобках числитель на знаменатель, для этого предварительно выполним манипуляции
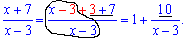
Подставим выражение в предел и превратим к 2 замечательному пределу
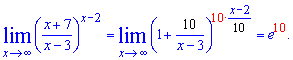
Предел равен экспоненте в 10 степени. Константы, которые являются слагаемыми при переменной как в скобках так и степени никакой "погоды" не вносят - об этом следует помнить. А если Вас спросят преподаватели - "Почему не превращаете показатель?" (Для этого примера в x-3), то скажите что "Когда переменная стремится к бесконечности то к ней хоть добавляй 100 хоть отнимай 1000, а предел останется такой как и был!".
Есть и второй способ вычислять пределы такого типа. О нем расскажем в следующем задании.
Пример 9. Найти предел
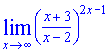 Решение: Теперь вынесем переменную в числителе и знаменателе и превратим оду особенность на другую. Для получения конечного значения используем формулу следствия 2 замечательного предела
Решение: Теперь вынесем переменную в числителе и знаменателе и превратим оду особенность на другую. Для получения конечного значения используем формулу следствия 2 замечательного предела
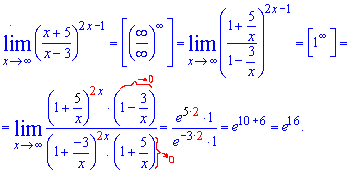
Пример 10. Найти предел функции
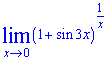 Решение: Заданный предел найти под силу не каждому. Для возведения под 2 предел представим, что sin (3x) это переменная, а нужно превратить показатель
Решение: Заданный предел найти под силу не каждому. Для возведения под 2 предел представим, что sin (3x) это переменная, а нужно превратить показатель
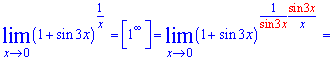
Далее показатель запишем как степень в степени
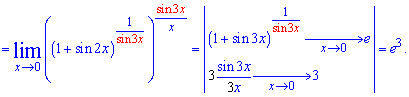
В скобках описаны промежуточные рассуждения. В результате использования первого и второго замечательного предела получили экспоненту в кубе.
Пример 11. Вычислить предел функции sin(2*x)/ln(3*x+1)
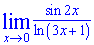 Решение: Имеем неопределенность вида 0/0. Кроме этого видим, что функцию следует превращать к использованию обеих замечательных пределов. Выполним предыдущие математические преобразования
Решение: Имеем неопределенность вида 0/0. Кроме этого видим, что функцию следует превращать к использованию обеих замечательных пределов. Выполним предыдущие математические преобразования
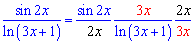
Далее без труда предел примет значение
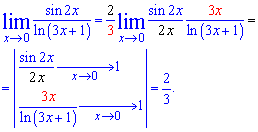
Вот так свободно Вы будете чувствовать себя на контрольных работах, тестах, модулях если научитесь быстро расписывать функции и сводить под первый или второй замечательный предел. Если заучить приведенные методики нахождения пределов Вам трудно, то всегда можете заказать контрольную работу на пределы у нас.
Для этого заполните форму, укажите данные и вложите файл с примерами. Мы помогли многим студентам - сможем помочь и Вам!