Законом распределения двух дискретных случайных величин называют перечень возможных значений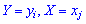 
и соответствующих им вероятностей совместного появления. В табличной форме этот закон имеет следующий вид
При подаче таблице использованы следующие обозначения
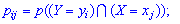
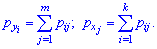
Условие нормировки для двух дискретных случайных величин имеет следующий вид:
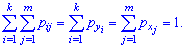
Основные числовые характеристики для случайных величин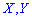 
, образующих систему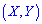 
Математическое ожидание определяется по формуле
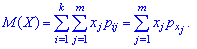
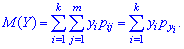
Дисперсия и среднее квадратическое отклонение для каждой дискретной величины определяют по правилам
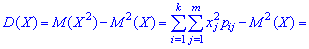
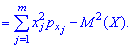
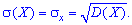
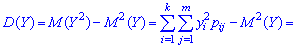
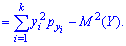
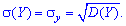
При изучении системы двух и более случайных величин приходится выяснять наличие связи между этими величинами и его характер. С соответствующей целью применяют корреляционный момент
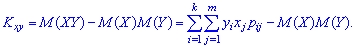
В случае нулевого значения корреляционного момента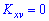 
связь между величинами 
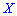и
, и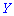, принадлежащих системе 
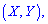отсутствует.
Когда момент отличен от нуля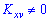 
, то между дискретными величинам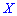и 
и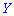 
существует корреляционная связь. Тесноту корреляционной связи характеризует коэффициент корреляции
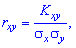
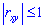, или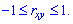 
Итак, если случайные величины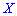 
и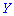 
независимы, то корреляционный момент равен нулю 
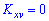и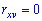 
. Равенство нулю 
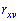является необходимым, но не достаточным условием независимости случайных величин. Может существовать система зависимых случайных величин, в которой коэффициент корреляции равен нулю. Примером такой системы является система двух случайных величин, которая равномерно распределена внутри круга радиусом 
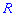с центром в начале координат. Две случайные величины 
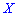и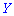 
называют некоррелированными, если коэффициент корреляции равен нулю 
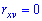, и коррелированными в противном случае 
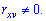Следовательно, если 
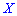и 
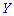независимы, то они будут и некоррелированными. Но с некоррелированности случайных величин в общем случае не следует их независимость.
-----------------------------------------
Приведем решение распространенного на практике примера.
Пример 1. Задан закон распределения системы двух дискретных случайных величин (X,Y):
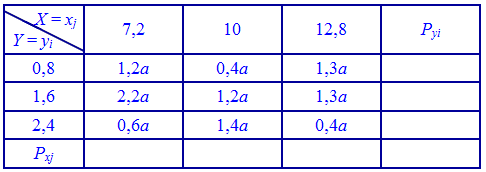
Найти неизвестную константу 
. Вычислить математическое ожидание, дисперсию и среднее матиматичне отклонения, корреляционный момент и коэффициент корреляции
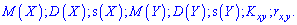
Решение. Применяя условие нормирования, находим каонстанту
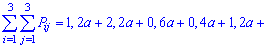
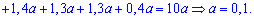
По найденным 
закон системы набирает такой вид:
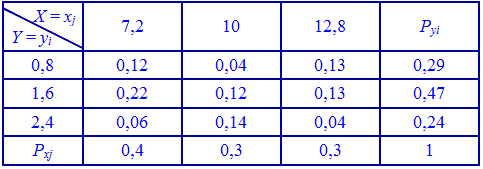
Основные числовые характеристики вычисляем по приведенным выше формулам. Математическое ожидание величины X получит значение
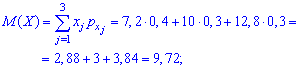
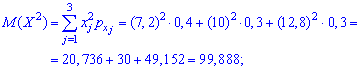
Дисперсия и среднее квадратичное отклонение набудут вида
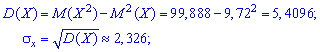
Аналогичные вычисления выполняем для нахождения числовых характеристик случайной величины Y
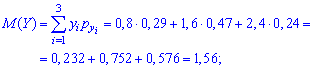
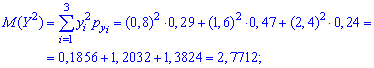
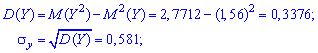
Находим математическое ожидание появления обоих событий
Значение корреляционного момента вычисляем по формуле
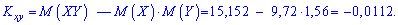
Поскольку корреляционный момент отличен от нуля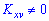 
, то между соответствующими величинами X и Y существует корреляционная связь.
Для измерения тесноты корреляционной связи вычислим коэффициент корреляции
-----------------------------
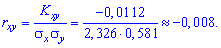
Подобных примеров можно найти немало в интернете и решебниках по теории вероятностей. Принцип их решения остается неизменным, поэтому хорошо проанализируйте приведенный пример. Если возникают трудности в вычислениях - обращайтесь, мы Вам поможем.
