Уравнением в полных дифференциалах называется уравнение вида
M(x,y)dx + N(x,y)dy = 0)
левая часть которого является полным дифференциалом некоторой функции
U(x,y), то есть dU(x,y) = M(x,y)dx + N(x,y)dy.
Напомним, что полный диференциал функции U находится по формуле
Условие проверки уравнения на соответствие полному дифференциалу имеет вид
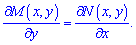(1)
Уравнение сводные к ДР в полных дифференциалах
В некоторых случаях зависимость
M(x,y)dx + N(x,y)dy = 0
не является уравнением в полных дифференциалах, не выполняется условие (1). Однако существует функция "мю"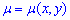 
такова, что если на нее умножить первоначальное уравнение 
то получим уравнением в полных дифференциалах.
Необходимым и достаточным условием этого является равенство между собой частных производных
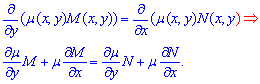
Функция "мю" называют интегрирующим множителем.
Таким образом кроме ДУ относительно функции u(x,y) на практике приходится решать дифференциальное уравнение в частных производных относительно интегрирующего множителя.
Но до сих пор остается открытым вопрос, как искать интегрирующий множитель?
Как найти интегрирующий множитель?
В теории обычно методика уже разработана и интегрирующий множитель следует искать в виде
где "омега" 
- известная функция одной или двоих переменных.
В этом случае получаем
После подстановки в условие полного дифференциала получим
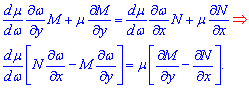Разделим переменные в последней строке
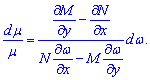Проинтегрировав и положив постоянную интегрирования равной нулю находим интегрирующий множитель
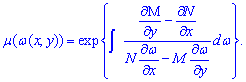Рассмотрим частные случаи.
1) Пусть "омега" равна аргументу. Тогда некоторые частные производные равны нулю, а интегрирующий множитель находят по формуле
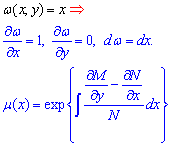2) Если "омега" ровна y то формула вычисления интегрирующего множителя имеет вид
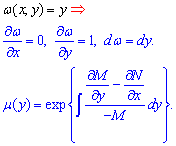3) В случае когда "омега" равна сумме или разности квадратов переменных интегрирующий множитель находим по формуле
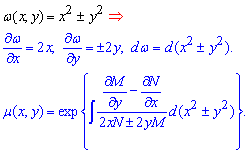4) И вариант когда имеем произведение переменных дает следующую зависимость для определения мю
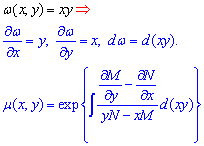Вывод формулы интегрирующего множителя без практики Вас ничего не научит, поэтому рассмотрим задачи из контрольной работы на которых Вы увидите суть всех приведенных выше формул. Примеры задавали во Львовском национальном университете им. И. Франка .
Уравнение в полных дифференциалах. Задача Коши.
Пример 1. Решить дифференциальное уравнение и задачу Коши
Решение: Выпишем множители при дифференциалах
и проверим выполняется ли условие полного дифференциала функции двух переменных
Как видим, левая часть уравнения не является полным дифференциалом (условие не выполняется). Проверим допускает ли дифференциальное уравнение интегрирующий множитель
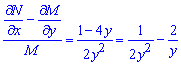
С правой стороны видим, что данное уравнение допускает множитель интегрирования, причем он зависит только от y.
Найдем интегрирующий множитель из дифференциального уравнения с отделенными переменными
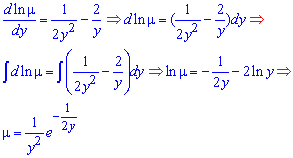
После умножения всех членов уравнения на найденный интегрирующий множитель "мю" (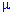
) получим Ду первого порядка
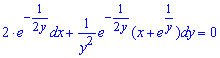
Если вновь проверить ДУ, то тепер условие на полный дифференциал некоторой функции выполняется
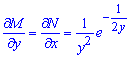
Далее будем решать полученное ДУ, как в случае обычного полного дифференциала. Проинтегрируем второе слагаемое по y
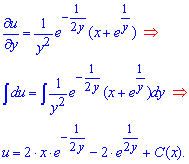
Запомните правило - если интегрирования идет по y, то сталая зависит от "икса", и наоборот.
Сталую которая входит в уравнения определяют вычислением частичной производной найденного решение по "икс" и приравниванием до множителя в ДУ при dx.
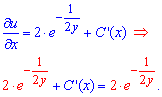
Отсюда находим постоянную
Учитывая все вышеизложенное, записываем общий интеграл дифференциального уравнения
В задании необходимо найти частичное решение (задачу Коши). Для этого записываем дополнительное условие на функцию и определяем сталую
Отсюда имеем частичное решение дифференциального уравнения
Оно пока записано в неявной форме, однако в этом случае можем найти зависимость функции от переменной y(x):
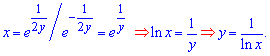- частичное решение дифференциального уравнения.
Пример 2.Найти решение задачи Коши
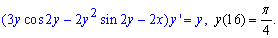Решение: Записываем заданное дифференциальное уравнение первого порядка в дифференциалах
Далее проверим имеем ли полный дифференциал, выписываем множители
и находим частные производные
Условие на полный дифференциал не выполняется.
Проверим не допускает это уравнение интегрирующего множителя
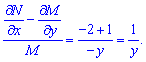
Видим что данное уравнение допускает интегрирующий множитель который зависит только от y. Найдем его интегрированием уравнения
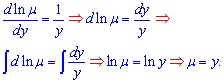
После умножения всех членов уравнения на найденный интегрирующий множитель исходное ДУ преобразуется к виду
что соответствует уравнению в полных дифференциалах
Как решить такое уравнение Вы уже знаете, поэтому переходим к интегрированию для простоты второго доданка (возле dx)
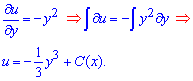
Чтобы определить постоянную - ищем частную производную функции u по "икс" и приравниваем ко второму множителя в полном дифференциале
На этот раз сталая функции не ровна константе и для ее установки нужно найти несколько интегралов
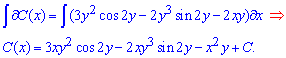
Общий интеграл дифференциального уравнения при подстановке C(x) примет вид
Решим задачу Коши для ДУ
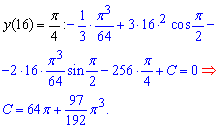
Отсюда имеем
- частичное решение дифференциального уравнения.
Пример 3. Найти решение уравнения при условии Коши
Решение: Перепишем ДУ расписав производную дифференциалами
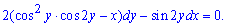
Далее действуем по методике для таких уравнений.
Выписываем множители возле дифференциалов
Проверяем условие на полный дифференциал функции
Условие не выполняется. Проверим, допускает ли интегрирующий множитель данное уравнение ?
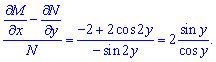
Как видим правая сторона зависима от y поэтому уравнение допускает интегрирующий множитель.
Найдем его из ДУ
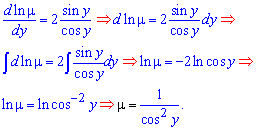
После умножения всех членов уравнения на интегрирующий множитель "мю" получим следующее уравнение
Условие полного дифференциала подтверждается
(
).
Далее применяем методику для ДУ в полных дифференциалах. С первого слагаемого уравнения интегрированием находим зависимость u(y)
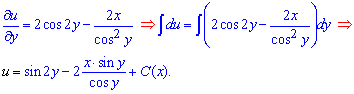
Далее вычисляем частную производную функции u(x,y) по "икс"
и сравниваем с частичной производной начального уравнения
Нетрудно найти отсюда константу
Возвращаемся и записываем общий интеграл дифференциального уравнения
По условию необходимо найти частичный интеграл уравнения (решить задачу Коши). Для этогоопределяем значение функции в точке
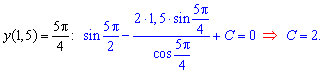
Константа равна 2, а частичное решение ДУ
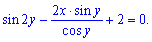
Для ясности ответа найдем (обратную) зависимость х(у):
- частичное решение уравнения
Красивый ответ несмотря на массу преобразований и интегралов.
Из приведенных ответов Вы получили полезную инструкцию для вычислений. Для проверки полученных знаний самостоятельно найдите решение уравнений, используя интегрирующий множитель
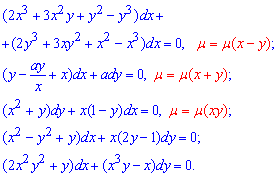Оставайтесь с нами, впереди еще много готовых примеров дифференциальных уравнений.
