Двойные и тройные интегралы

Двойные и тройные интегралы даются трудно всем студентам. Одна из причин - это отсутствие возможности качественно строить области интегрирования.
Из воображения их брать удается не многим специалистам. Что касается нахождения объемов, образованных пересечением плоскостей, то здесь эта проблема становится еще большей.
Другое дело, что часто кратные интегралы начинают изучать когда студенты только что научились находить определенные интегралы.
Всем Вам помогут в учебе готовые ответы индивидуальной работы.
Приведенные ниже 10 примеров научат Вас решать задание разной сложности.

ВАРИАНТ - 19

Двойной интеграл

ЗАДАНИЕ 1.14 Поменять порядок интегрирования в двойном интеграле:

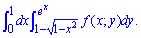
Решение: Из интеграла выписываем область интегрирования, которая ограничена кривыми

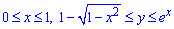
где 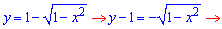(y - 1)²=1 - x², x²+(y - 1)²=1.
Получили нижний полукруг с центром в точке O (0;1) и радиусом R=1.
Выражаем полученные функции через переменную y:
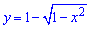, отсюда 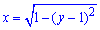перед радикалом стоит знак "+" поскольку часть круга находится в правой (положительной по x) части полплоскости;
y=e^x, отсюда x=ln (y).
Выполняем построение рисунка к задаче, это служит доброй подсказкой при выполнении заданий


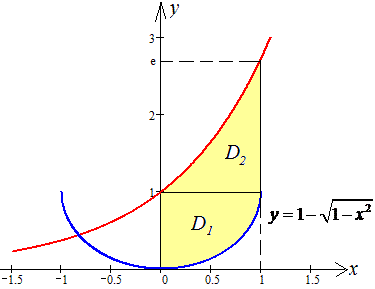
Как изменять пределы интегрирования Вас по-видимому учили.
Если не все знают, то просто мнимо проведите прямую и выпишите закон за которым изменяются края при прохождении кривой снизу вверх, или слева направо. Таким образом Вы будете знать и количество областей разбития, и функции, которые ограничивают площадь или объем тела.
При изменении порядка интегрирования нашу область разбили на две области: D=D₁+D₂.
Расставим пределы интегрирования в каждой области:

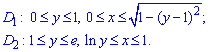
Еще раз внимательно пересмотрите рисунок и попробуйте проанализировать почему так.
При изменении порядка интегрирования получим два двойных интеграла
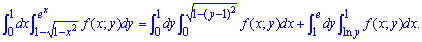На этом и все объяснения к первой задаче.

ЗАДАНИЕ 2.13 Найти площадь плоской фигуры, заданной следующими условиями, : xy=1, xy=2, 6y=7-x.
Решение: Сначала выполняем построение кривых, чтобы понять площадь какой фигуры ищем

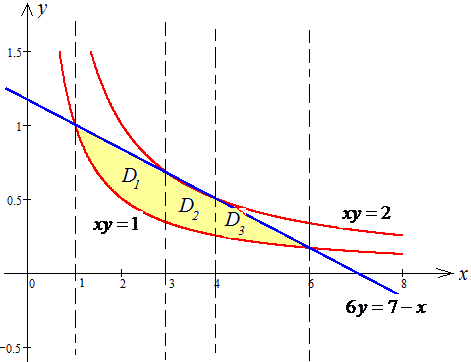
Дальше видим, что область интегрирования нужно разбивать на три части.
Есть другой вариант, более легкий с точки зрения практической реализации.
Можно найти площадь между двумя красными кривыми и от нее отнять площадь в области D₂ между красной и синей кривыми. В результате получим разницу двух двойных интегралов.
Но здесь пойдем более длинным по пути, описанный попробуйте реализовать самостоятельно.
Первое, что нам нужно - это определить в каких точках графика кривые пересекают друг друга.
Найдем точки пересечения графиков 1 и 3 функций:
складываем систему из двух уравнений

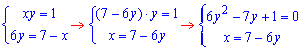
и находим решение 

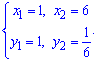
Пересечение второй и третьей функций дают систему уравнений

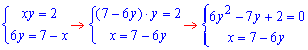
для определения двух точек

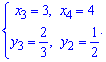
Заданную область будем разбивать на три области: D=D₁+D₂+D₃.
Расставим пределы интегрирования в каждой области:

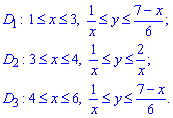
Через двойной интеграл вычисляем площадь фигуры, ограниченной заданными кривыми:
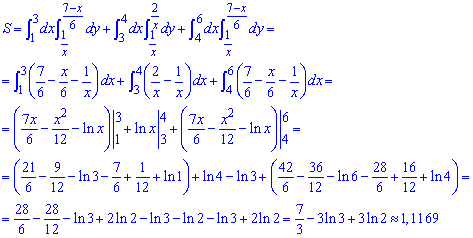Интеграл в итоге дает много логарифмов, которые группируем.
Приближенно площадь поверхности равна 1,12 единиц квадратных.

ЗАДАНИЕ 3.12 Вычислить двойной интеграл по области D, ограниченной указанными линиями: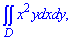
D: y=2x³, y=0, x=1.
Решение: Найдем точки пересечения графиков заданных функций : 2x³=0, x=0.
Изобразим графически область интегрирования

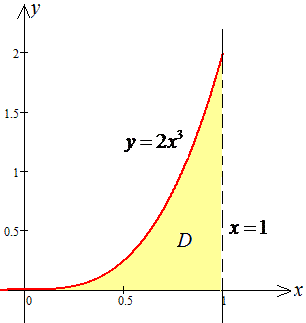
Расставим пределы в заданной области D:

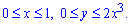
Вычислим двойной интеграл по области D, ограниченной указанными линиями: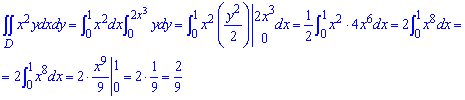
Напомним, что это есть лишь двойной интеграл.
Площадь имеет место лишь в тех случаях, когда функция интегрирования равна единице.

ЗАДАНИЕ 4.11 Вычислить двойной интеграл, используя полярные координаты:

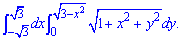
Решение: Запишем область интегрирования, которая ограничена кривыми

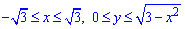
где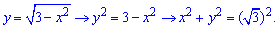
Получили круг с центром в точке O (0;0) и радиусом ровным ругаю из трех 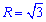(верхняя половина).
Изобразим полукруг в декартовой и полярной системе координат

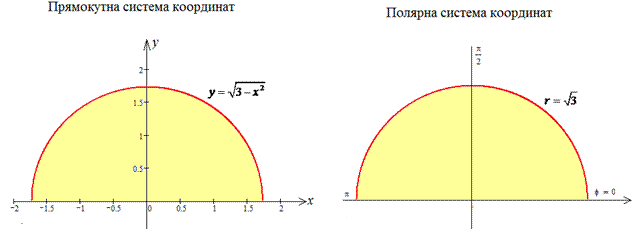
Перейдем к полярной системе координат (СК), используя следующую замену переменных :

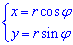
Следует помнить, что дополнительно нужно вычислить якобиан перехода от декартовой к полярной СК:

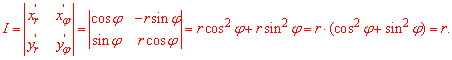
Он важен, поскольку на него нужно домножити подинтегральную функцию, выраженную в новых координатах
Найдем вид подинтегральной функции в полярной системе координат :

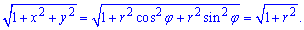
Запишем пределы интегрирования в полярной СК:

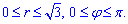
Осталось вычислить двойной интеграл:

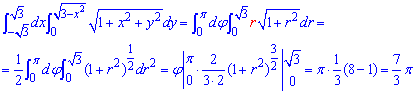
Интеграл равен I=7*Pi/3.
То, что интеграл содержит число Pi лишь подтверждает правильность вычислений, ведь для круговых форм это распространено.

ЗАДАНИЕ 5.10 Вычислить площадь области D, ограниченной указанными линиями:
D: y=x²+2, x=2, y=x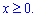

Решение: Расставим пределы в заданной области D:

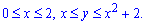
Построим кривые, чтобы представить фигуру площадь которой мы ищем.

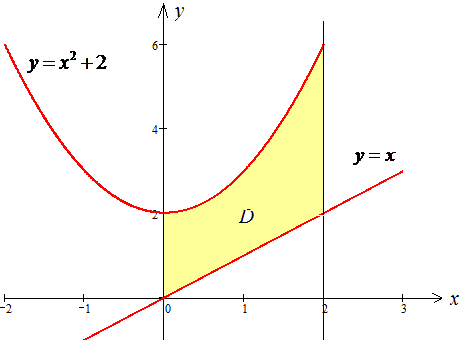
Здесь есть два варианта: сложный - когда внутренний интеграл за переменной x предусматривает нахождение площади, через сумму двойных интегралов по 2 или 3 областям.
Мы же пойдем легким по пути и определим площадь заштрихованной фигуры с помощью одного двойного интеграла.
Вычислим площадь криволинейной трапеции, ограниченной указанными линиями: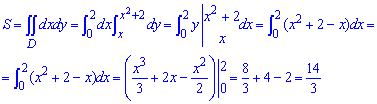

Площадь равна S=14/3 единиц квадратных.
Как видите - выбор порядка интегрирования может существенно сэкономить время при написании контрольной работы, на экзамене или практических заданиях. Для сравнения попробуйте вычислить первым временем и сравнить масштаб выполненных работ.

ЗАДАНИЕ 6.9 Используя двойной интеграл, вычислить, перейдя к полярным координатам, площадь плоской фигуры : (x²+y²)²=a²(2x²+3y²).
Решение: Один из предыдущих примеров содержал переход к полярной системе координат :

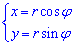
и был найден якобиан переходу I=r.
Определим пределы интегрирования :

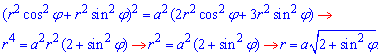
Пределы интегрирования: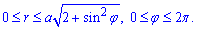
Их легко определить в полярной СК - радиус изменяется от нуля к кривой, которая ограничивает площадь, а угол изменяется от 0 до 360 градусов.
Это Вы должны знать при вычислении подобных заданий.
Вычислим площадь плоской фигуры:

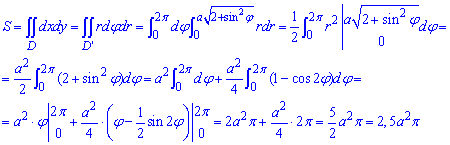
Под интегралом пришлось понижать степень синуса за известной тригонометрической формулой. На пратиці Вы такие случаи рассматривали, то же здесь мы Вам ничего нового не открываем.

ЗАДАНИЕ 7.8 Найти объем тела, заданного поверхностями, что его ограничивают:
y=7-x²-z², 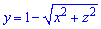, y=0.
Решение: Половину 3d рисунка тела изобразим графически - это хорошая подсказка, которая развивает воображение.

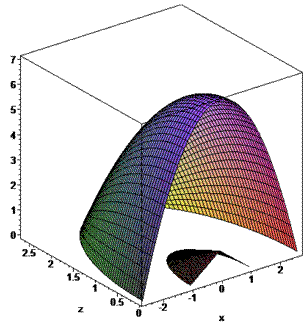
Вычислим объем тела, которое ограничивает эти две поверхности (то есть рисунок разрезали пополам для наглядного отражения)+ снизу плоскостью y=0.
Чтобы упростить интегралы объем тела найдем как разницу объемов параболоида и конуса (см. рис.).

Расставим пределы в заданной области D₁ (круг радиусом ):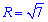

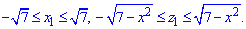
Найдем объем параболоида:

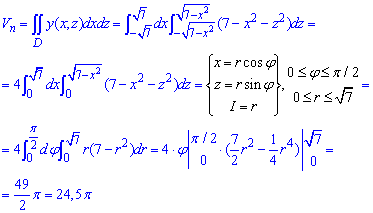
При нахождении двойного интегралу целесообразно перейти к полярной СК, поскольку обе фигуры образованы вращением кривой вокруг оси Oy.
Расставим пределы в области D₂ (круг радиусом R=1):

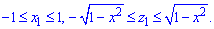
Вычислим объем конуса:

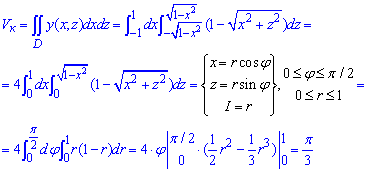
Он равен V=Pi/3 единиц кубических.
Здесь также во время интегрирования перешли к полярной СК.
Последним шагом найдем объем тела, которое находится между параболоидом и конусом, :
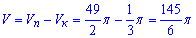Разница объемов равна V=145*Pi/6=75,88 единиц кубических.

Тройной интеграл

ЗАДАНИЕ 8.7 Расставить пределы интегрирования в тройном интеграле 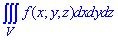, если область V ограничена указанными поверхностями:
V: 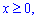y=2x, y=1 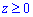, x+y+z=3.
Нарисовать область интегрирования.
Решение: В плоскости Oxy уравнение прямых запишем следующим образом: y=1, x=y/2, x=3-y.
Уравнение плоскости в пространстве запишем в виде: z=3-y-x.
Построим пространственный рисунок тела и его проекцию в декартовую плоскость
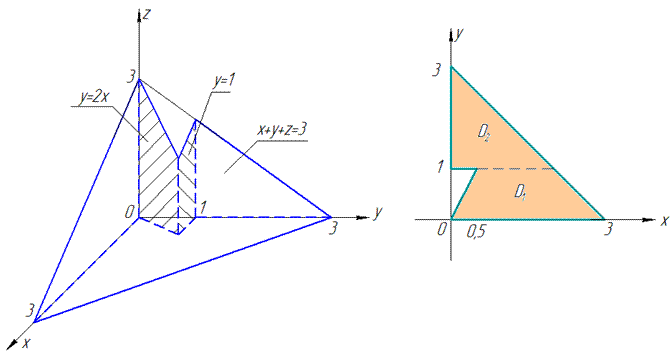Как видно из рисунку область тела D, что проектируется на плоскость Oxy, разбивается на две части:
D=D₁+D₂, поэтому пределы интегрирования расставляем следующим образом:

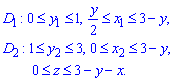
На основе проведенного анализа записываем пределы в тройной интеграл
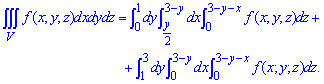Внимательно разберите как изменятся пределы, если интегрировать за переменной y во внутреннем интеграле.
Легко убедиться, что получим сумму из трех тройных интегралов.

ЗАДАНИЕ 9.6 Вычислить тройные интегралы: 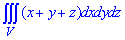где область интегрирования ограничена: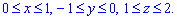
Решение: Область являет собой параллелепипед, который изображен ниже

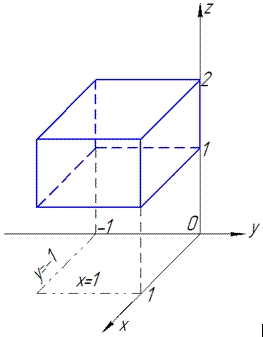
Это значительно упрощает интегрирование
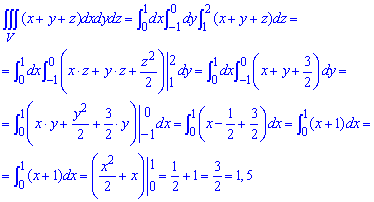Детали вычислений хорошо расписаны в формулах, потому здесь важно лишь правильно подставить пределы и не ошибиться при грустит.

ЗАДАНИЕ 10.5 Используя тройной интеграл, вычислить объем тела, ограниченного поверхностями:

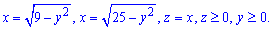
Нарисовать область интегрирования.
Решение: Прежде всего выполняем построение к условию, в крайнем случае старайтесь схематически нарисовать область интегрирования

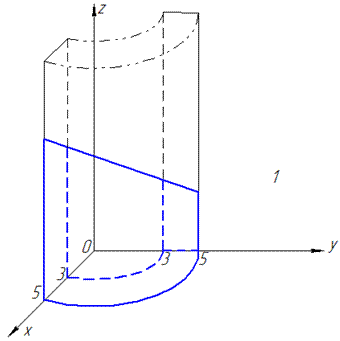
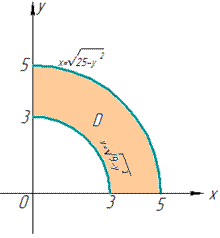
Дальше записываем пределы интегрирования, учитывая выполненный рисунок:

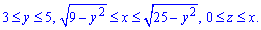
Через тройной интеграл находим объем тела:

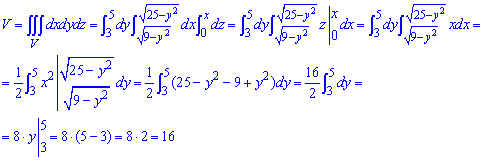
Превращения не сложны и их разберите самостоятельно.
Объем ровный 16 куб. од.
На этом индивидуальная работа из повторных интегралов выполнена.
Больше примеров на двойные и тройные интегралы Вы можете найти в следующих материалах.